Yuan-chin Ivan Chang
Determination of class-specific variables in nonparametric multiple-class classification
May 07, 2022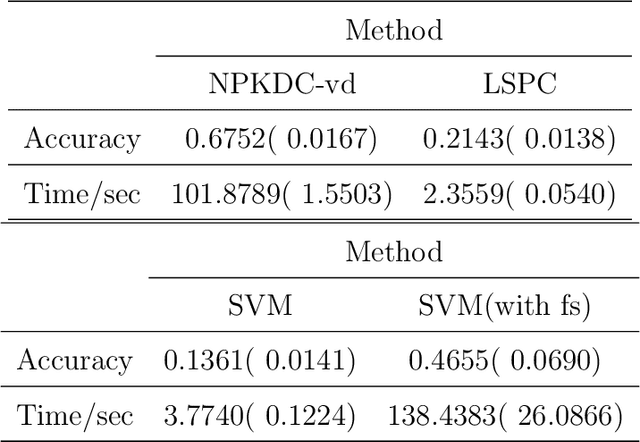
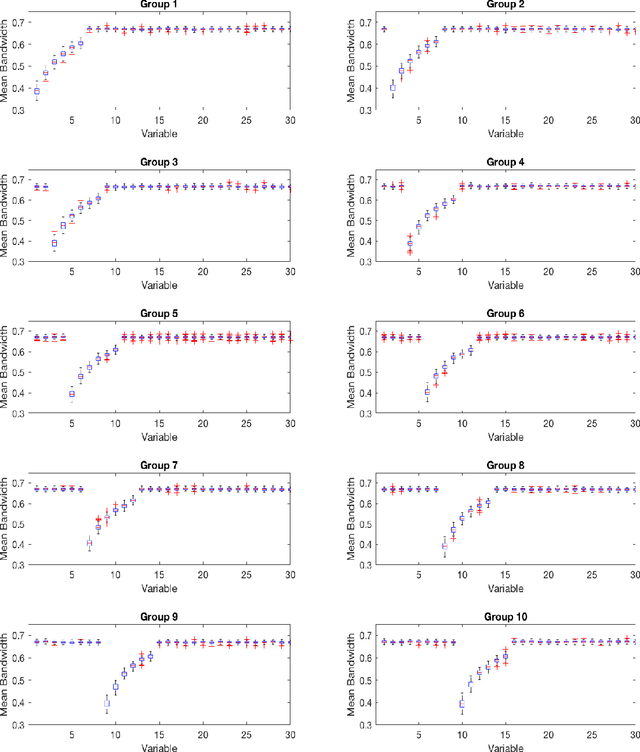
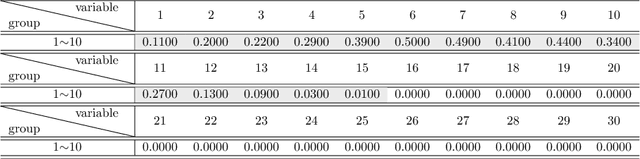
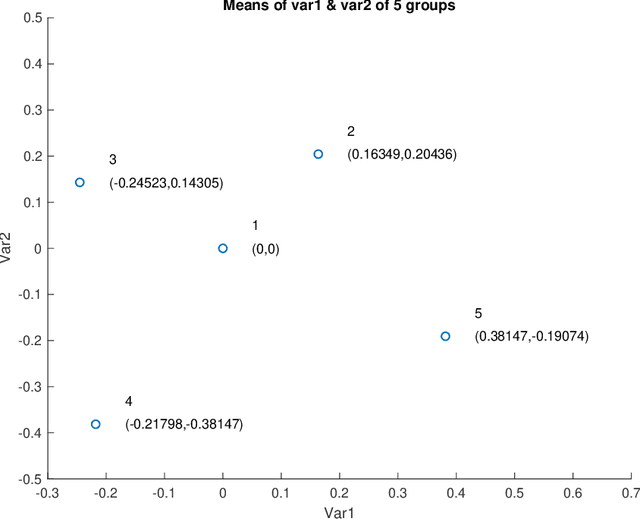
Abstract:As technology advanced, collecting data via automatic collection devices become popular, thus we commonly face data sets with lengthy variables, especially when these data sets are collected without specific research goals beforehand. It has been pointed out in the literature that the difficulty of high-dimensional classification problems is intrinsically caused by too many noise variables useless for reducing classification error, which offer less benefits for decision-making, and increase complexity, and confusion in model-interpretation. A good variable selection strategy is therefore a must for using such kinds of data well; especially when we expect to use their results for the succeeding applications/studies, where the model-interpretation ability is essential. hus, the conventional classification measures, such as accuracy, sensitivity, precision, cannot be the only performance tasks. In this paper, we propose a probability-based nonparametric multiple-class classification method, and integrate it with the ability of identifying high impact variables for individual class such that we can have more information about its classification rule and the character of each class as well. The proposed method can have its prediction power approximately equal to that of the Bayes rule, and still retains the ability of "model-interpretation." We report the asymptotic properties of the proposed method, and use both synthesized and real data sets to illustrate its properties under different classification situations. We also separately discuss the variable identification, and training sample size determination, and summarize those procedures as algorithms such that users can easily implement them with different computing languages.
Active learning for binary classification with variable selection
Jan 29, 2019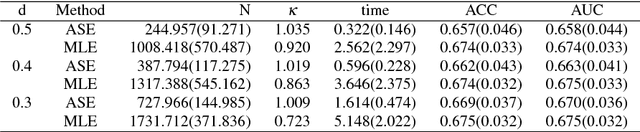
Abstract:Modern computing and communication technologies can make data collection procedures very efficient. However, our ability to analyze large data sets and/or to extract information out from them is hard-pressed to keep up with our capacities for data collection. Among these huge data sets, some of them are not collected for any particular research purpose. For a classification problem, this means that the essential label information may not be readily obtainable, in the data set in hands, and an extra labeling procedure is required such that we can have enough label information to be used for constructing a classification model. When the size of a data set is huge, to label each subject in it will cost a lot in both capital and time. Thus, it is an important issue to decide which subjects should be labeled first in order to efficiently reduce the training cost/time. Active learning method is a promising outlet for this situation, because with the active learning ideas, we can select the unlabeled subjects sequentially without knowing their label information. In addition, there will be no confirmed information about the essential variables for constructing an efficient classification rule. Thus, how to merge a variable selection scheme with an active learning procedure is of interest. In this paper, we propose a procedure for building binary classification models when the complete label information is not available in the beginning of the training stage. We study an model-based active learning procedure with sequential variable selection schemes, and discuss the results of the proposed procedure from both theoretical and numerical aspects.
Fast Multi-Class Probabilistic Classifier by Sparse Non-parametric Density Estimation
Jan 04, 2019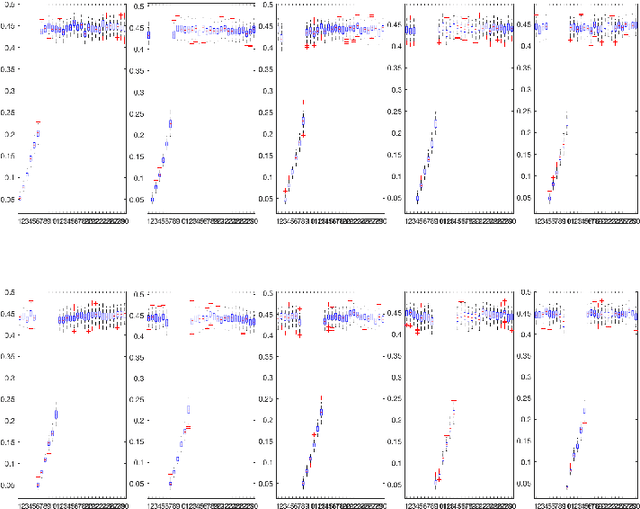
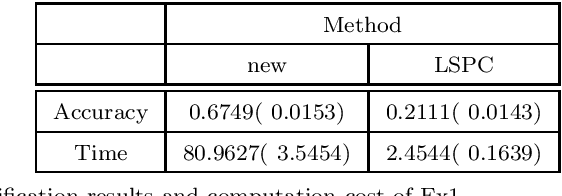
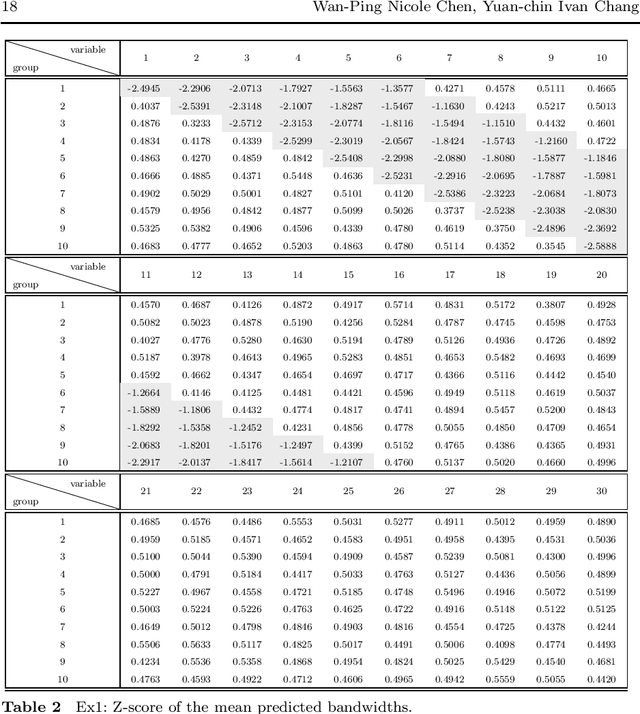
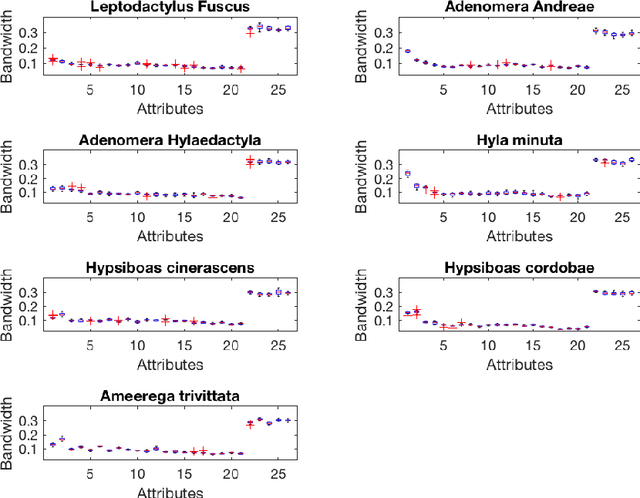
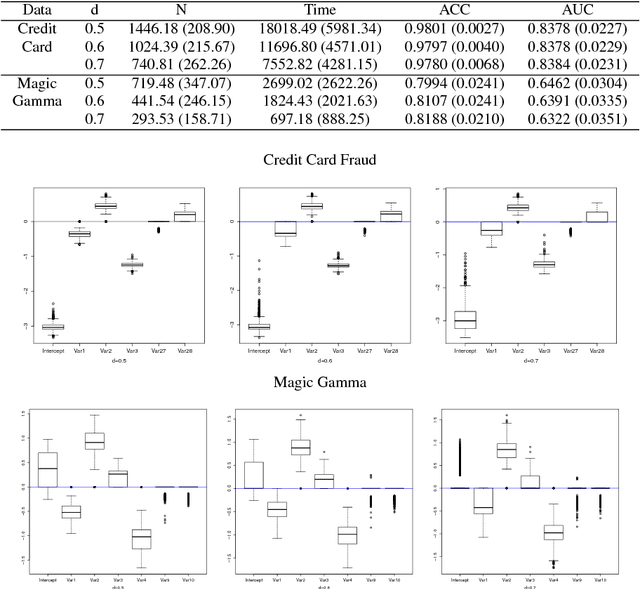
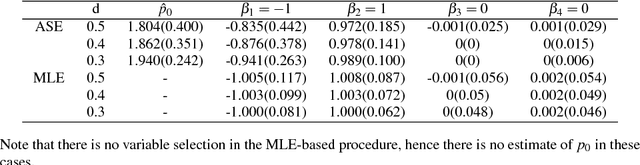
Abstract:The model interpretation is essential in many application scenarios and to build a classification model with a ease of model interpretation may provide useful information for further studies and improvement. It is common to encounter with a lengthy set of variables in modern data analysis, especially when data are collected in some automatic ways. This kinds of datasets may not collected with a specific analysis target and usually contains redundant features, which have no contribution to a the current analysis task of interest. Variable selection is a common way to increase the ability of model interpretation and is popularly used with some parametric classification models. There is a lack of studies about variable selection in nonparametric classification models such as the density estimation-based methods and this is especially the case for multiple-class classification situations. In this study we study multiple-class classification problems using the thought of sparse non-parametric density estimation and propose a method for identifying high impacts variables for each class. We present the asymptotic properties and the computation procedure for the proposed method together with some suggested sample size. We also repost the numerical results using both synthesized and some real data sets.
Distributed sequential method for analyzing massive data
Dec 22, 2018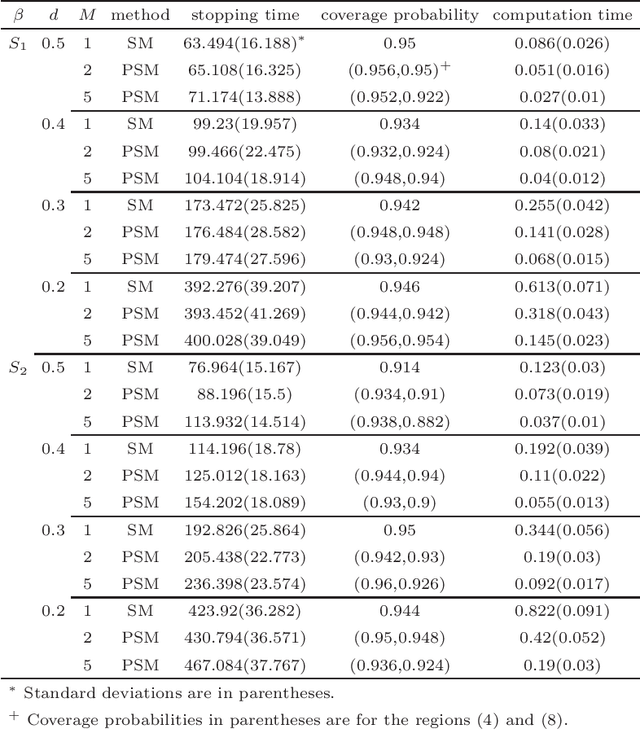
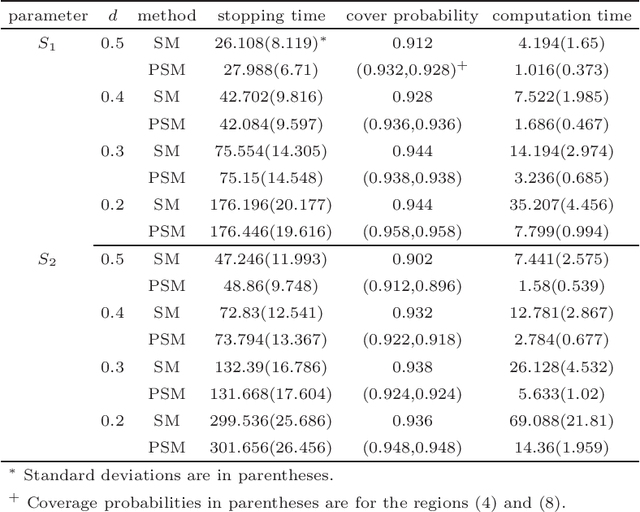
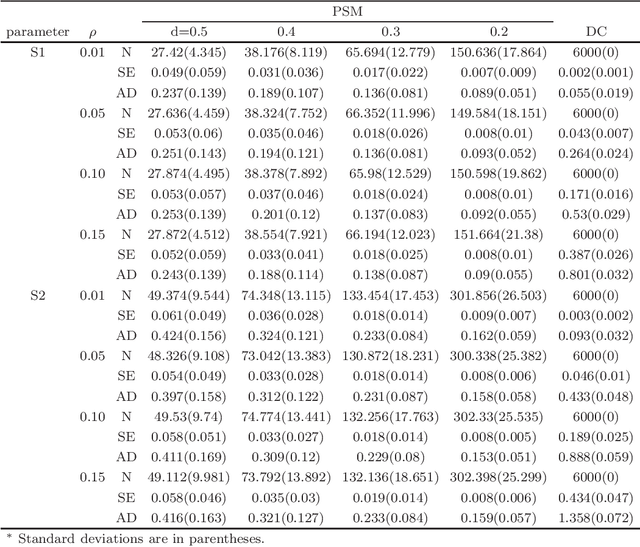
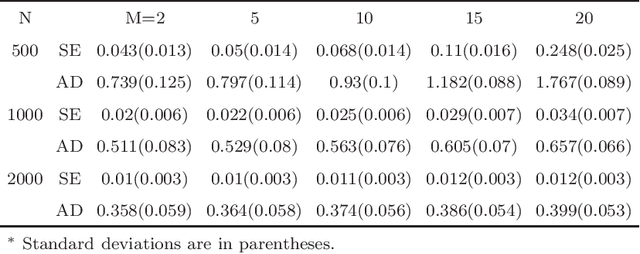
Abstract:To analyse a very large data set containing lengthy variables, we adopt a sequential estimation idea and propose a parallel divide-and-conquer method. We conduct several conventional sequential estimation procedures separately, and properly integrate their results while maintaining the desired statistical properties. Additionally, using a criterion from the statistical experiment design, we adopt an adaptive sample selection, together with an adaptive shrinkage estimation method, to simultaneously accelerate the estimation procedure and identify the effective variables. We confirm the cogency of our methods through theoretical justifications and numerical results derived from synthesized data sets. We then apply the proposed method to three real data sets, including those pertaining to appliance energy use and particulate matter concentration.
Evaluating the diagnostic powers of variables and their linear combinations when the gold standard is continuous
May 09, 2011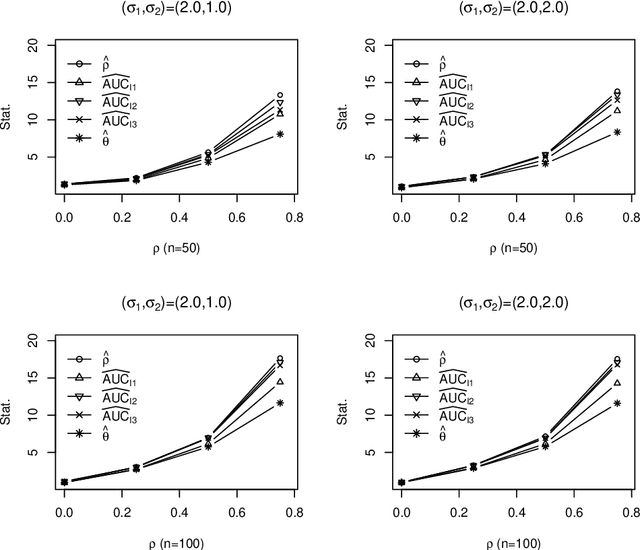
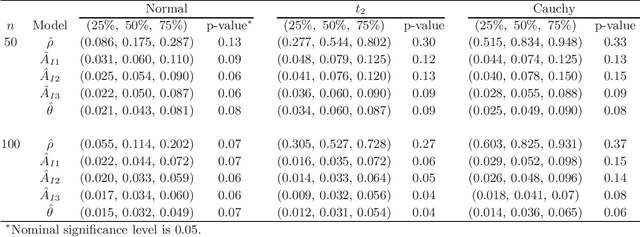
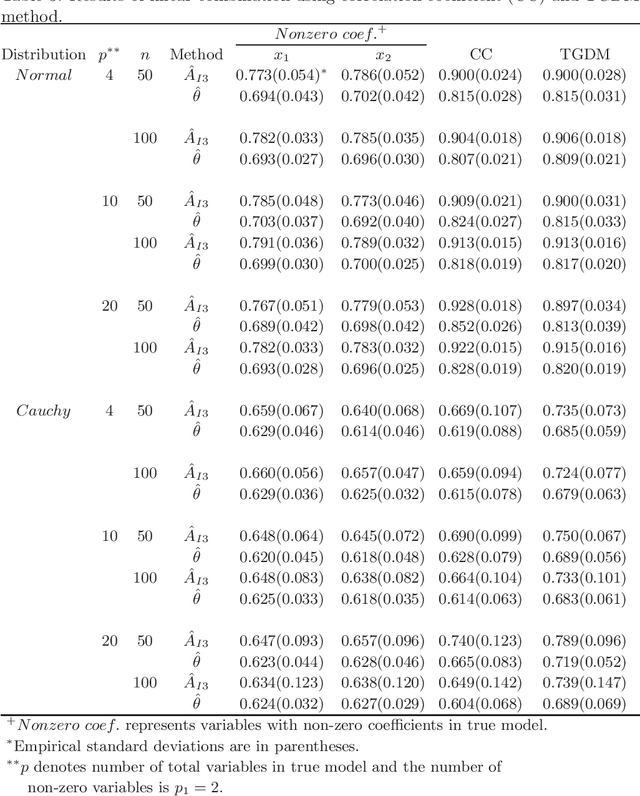
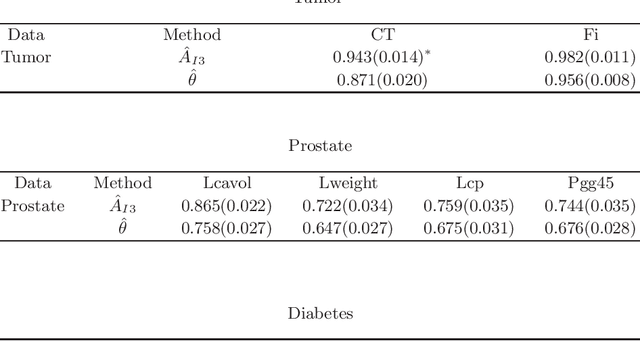
Abstract:The receiver operating characteristic (ROC) curve is a very useful tool for analyzing the diagnostic/classification power of instruments/classification schemes as long as a binary-scale gold standard is available. When the gold standard is continuous and there is no confirmative threshold, ROC curve becomes less useful. Hence, there are several extensions proposed for evaluating the diagnostic potential of variables of interest. However, due to the computational difficulties of these nonparametric based extensions, they are not easy to be used for finding the optimal combination of variables to improve the individual diagnostic power. Therefore, we propose a new measure, which extends the AUC index for identifying variables with good potential to be used in a diagnostic scheme. In addition, we propose a threshold gradient descent based algorithm for finding the best linear combination of variables that maximizes this new measure, which is applicable even when the number of variables is huge. The estimate of the proposed index and its asymptotic property are studied. The performance of the proposed method is illustrated using both synthesized and real data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge