RETQA: A Large-Scale Open-Domain Tabular Question Answering Dataset for Real Estate Sector

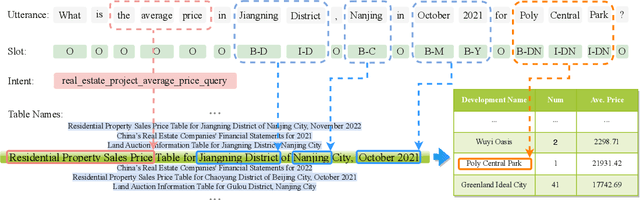
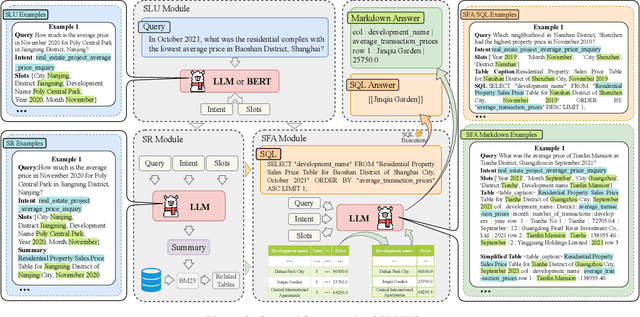
The real estate market relies heavily on structured data, such as property details, market trends, and price fluctuations. However, the lack of specialized Tabular Question Answering datasets in this domain limits the development of automated question-answering systems. To fill this gap, we introduce RETQA, the first large-scale open-domain Chinese Tabular Question Answering dataset for Real Estate. RETQA comprises 4,932 tables and 20,762 question-answer pairs across 16 sub-fields within three major domains: property information, real estate company finance information and land auction information. Compared with existing tabular question answering datasets, RETQA poses greater challenges due to three key factors: long-table structures, open-domain retrieval, and multi-domain queries. To tackle these challenges, we propose the SLUTQA framework, which integrates large language models with spoken language understanding tasks to enhance retrieval and answering accuracy. Extensive experiments demonstrate that SLUTQA significantly improves the performance of large language models on RETQA by in-context learning. RETQA and SLUTQA provide essential resources for advancing tabular question answering research in the real estate domain, addressing critical challenges in open-domain and long-table question-answering. The dataset and code are publicly available at \url{https://github.com/jensen-w/RETQA}.

A deep Convolutional Neural Network for topology optimization with strong generalization ability

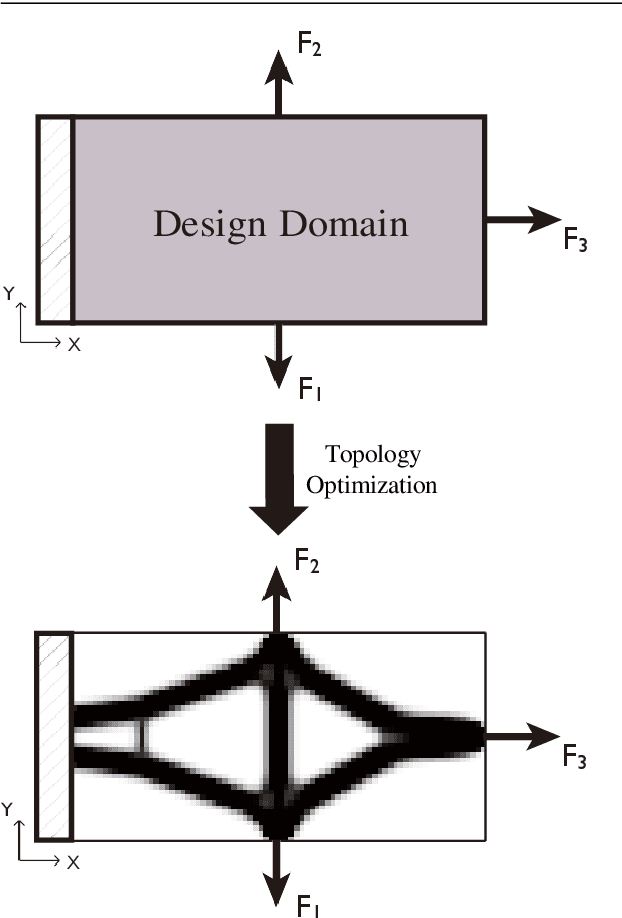
This paper proposes a deep Convolutional Neural Network(CNN) with strong generalization ability for structural topology optimization. The architecture of the neural network is made up of encoding and decoding parts, which provide down- and up-sampling operations. In addition, a popular technique, namely U-Net, was adopted to improve the performance of the proposed neural network. The input of the neural network is a well-designed tensor with each channel includes different information for the problem, and the output is the layout of the optimal structure. To train the neural network, a large dataset is generated by a conventional topology optimization approach, i.e. SIMP. The performance of the proposed method was evaluated by comparing its efficiency and accuracy with SIMP on a series of typical optimization problems. Results show that a significant reduction in computation cost was achieved with little sacrifice on the optimality of design solutions. Furthermore, the proposed method can intelligently solve problems under boundary conditions not being included in the training dataset.