Yini Zhang
Targeted sampling from massive Blockmodel graphs with personalized PageRank
Oct 04, 2019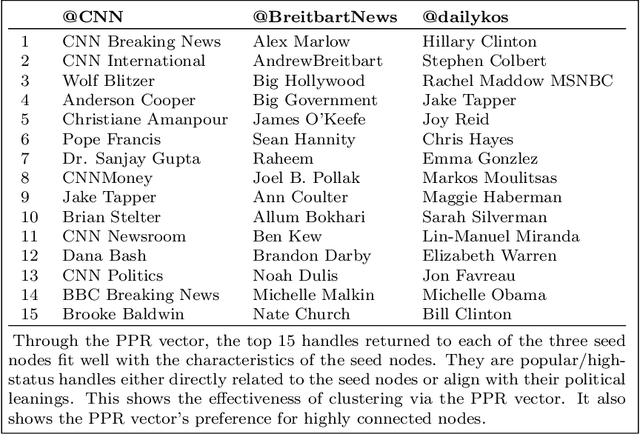
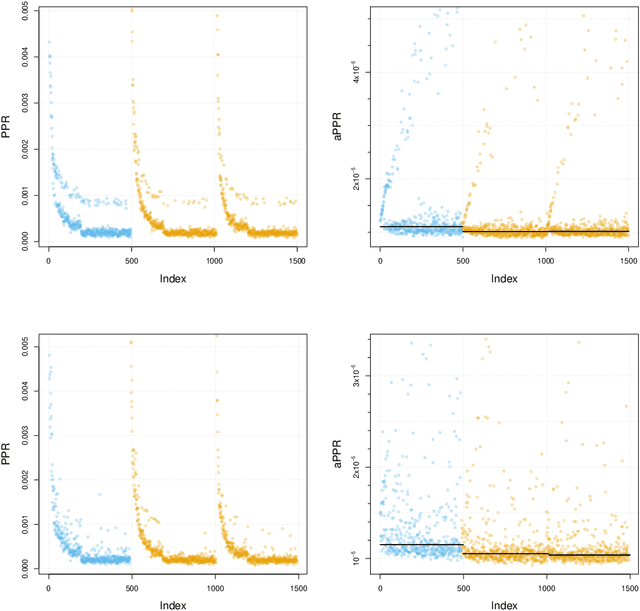

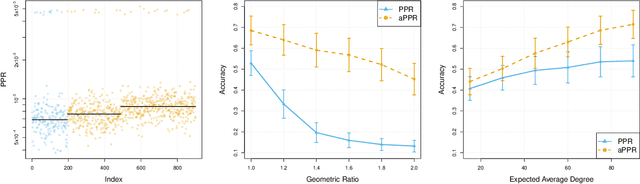
Abstract:This paper provides statistical theory and intuition for Personalized PageRank (PPR), a popular technique that samples a small community from a massive network. We study a setting where the entire network is expensive to thoroughly obtain or maintain, but we can start from a seed node of interest and "crawl" the network to find other nodes through their connections. By crawling the graph in a designed way, the PPR vector can be approximated without querying the entire massive graph, making it an alternative to snowball sampling. Using the Degree-Corrected Stochastic Blockmodel, we study whether the PPR vector can select nodes that belong to the same block as the seed node. We provide a simple and interpretable form for the PPR vector, highlighting its biases towards high degree nodes outside of the target block. We examine a simple adjustment based on node degrees and establish consistency results for PPR clustering that allows for directed graphs. We illustrate the method with the Twitter friendship graph and find that (i) the adjusted and unadjusted PPR techniques are complementary approaches, where the adjustment makes the results particularly localized around the seed node and (ii) the bias adjustment greatly benefits from degree regularization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge