Effective Out-of-Distribution Detection in Classifier Based on PEDCC-Loss

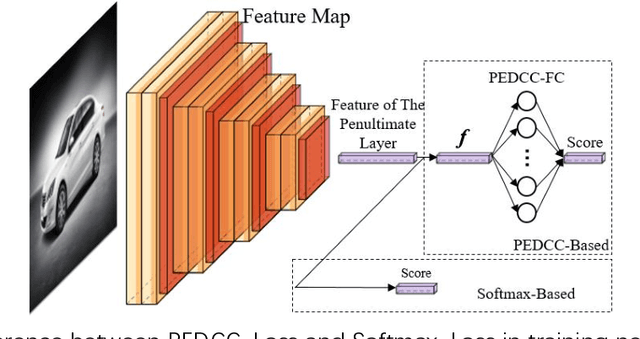
Deep neural networks suffer from the overconfidence issue in the open world, meaning that classifiers could yield confident, incorrect predictions for out-of-distribution (OOD) samples. Thus, it is an urgent and challenging task to detect these samples drawn far away from training distribution based on the security considerations of artificial intelligence. Many current methods based on neural networks mainly rely on complex processing strategies, such as temperature scaling and input preprocessing, to obtain satisfactory results. In this paper, we propose an effective algorithm for detecting out-of-distribution examples utilizing PEDCC-Loss. We mathematically analyze the nature of the confidence score output by the PEDCC (Predefined Evenly-Distribution Class Centroids) classifier, and then construct a more effective scoring function to distinguish in-distribution (ID) and out-of-distribution. In this method, there is no need to preprocess the input samples and the computational burden of the algorithm is reduced. Experiments demonstrate that our method can achieve better OOD detection performance.

Generation and frame characteristics of predefined evenly-distributed class centroids for pattern classification

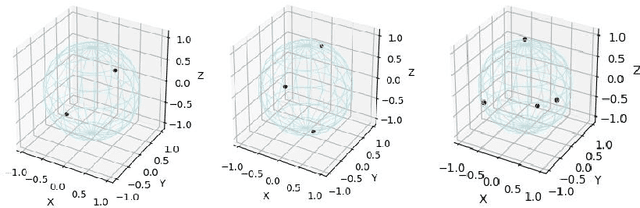
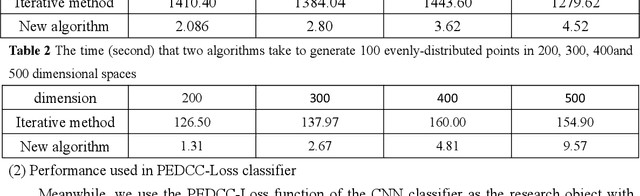
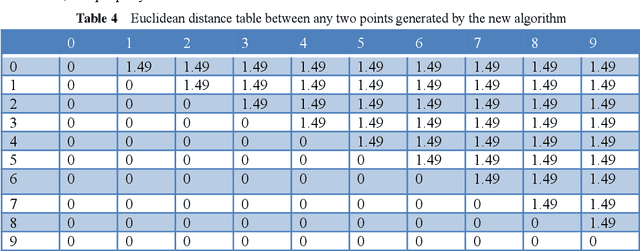
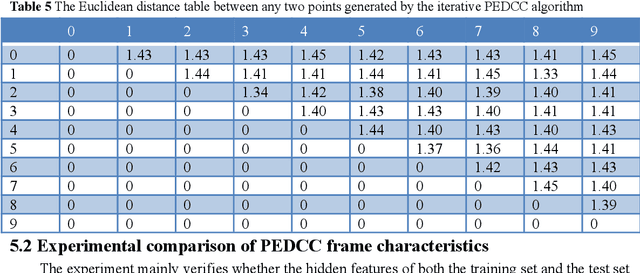
Predefined evenly-distributed class centroids (PEDCC) can be widely used in models and algorithms of pattern classification, such as CNN classifiers, classification autoencoders, clustering, and semi-supervised learning, etc. Its basic idea is to predefine the class centers, which are evenly-distributed on the unit hypersphere in feature space, to maximize the inter-class distance. The previous method of generating PEDCC uses an iterative algorithm based on a charge model, that is, the initial values of various centers (charge positions) are randomly set from the normal distribution, and the charge positions are updated iteratively with the help of the repulsive force between charges of the same polarity. The class centers generated by the algorithm will produce some errors with the theoretically evenly-distributed points, and the generation time will be longer. This paper takes advantage of regular polyhedron in high-dimensional space and the evenly distribution of points on the n dimensional hypersphere to generate PEDCC mathematically. Then, we discussed the basic and extensive characteristics of the frames formed by PEDCC. Finally, experiments show that new algorithm is not only faster than the iterative method, but also more accurate in position. The mathematical analysis and experimental results of this paper can provide a theoretical tool for using PEDCC to solve the key problems in the field of pattern recognition, such as interpretable supervised/unsupervised learning, incremental learning, uncertainty analysis and so on.