Joint Time-Position Statistics and Fisher Information in Drift-Diffusion Molecular Channels

This letter presents a closed-form characterization of the joint distribution of first arrival time (FAT) and first arrival position (FAP) in diffusion-based molecular communication (MC) systems with drift. Prior studies have investigated FAT modeling via inverse Gaussian distributions [1] and applied FAT statistics for parameter estimation and synchronization tasks [2], [3], while more recent work has characterized FAP for spatial channel analysis [4]. In contrast, we derive an explicit joint probability density function (PDF) under constant drift and isotropic diffusion in arbitrary spatial dimensions. Our result reveals a nontrivial coupling between arrival time and lateral position, generalizing known inverse Gaussian models. We further compute the Fisher information matrix (FIM) with respect to key channel parameters, showing that the joint observation enables estimation of lateral drift and improves sensitivity to the diffusion coefficient -- capabilities not achievable with time-only or position-only models. This joint framework enhances the modeling and inference capabilities for molecular communication channels where spatial randomness itself carries non-negligible information.

Capacity of First Arrival Position Channel in Diffusion-Based Molecular Communication

In [1], the impulse response of the first arrival position (FAP) channel of 2D and 3D spaces in molecular communication (MC) is derived, but its Shannon capacity remains open. The main difficulty of depicting the FAP channel capacity comes from the fact that the FAP density becomes a multi-dimensional Cauchy distribution when the drift velocity approaches zero. As a result, the commonly used techniques in maximizing the mutual information no longer work because the first and second moments of Cauchy distributions do not exist. Our main contribution in this paper is a complete characterization of the zero-drift FAP channel capacity for the 2D and 3D spaces. The capacity formula for FAP channel turns out to have a similar form compared to the Gaussian channel case (under second-moment power constraint). It is also worth mentioning that the capacity value of 3D FAP channel is twice as large as 2D FAP channel. This is an evidence that the FAP channel has larger capacity as the spatial dimension grows. Finally, our technical contributions are the application of a modified logarithmic constraint as a replacement of the usual power constraint, and the choice of output signal constraint as a substitution to input signal constraint in order to keep the resulting formula concise.

First Arrival Position in Molecular Communication Via Generator of Diffusion Semigroup

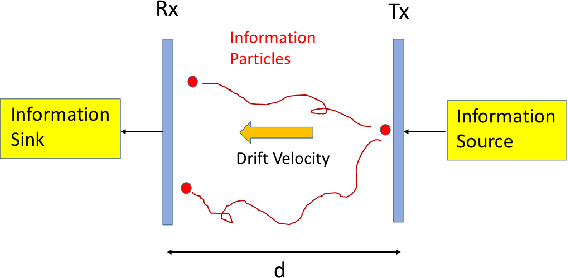
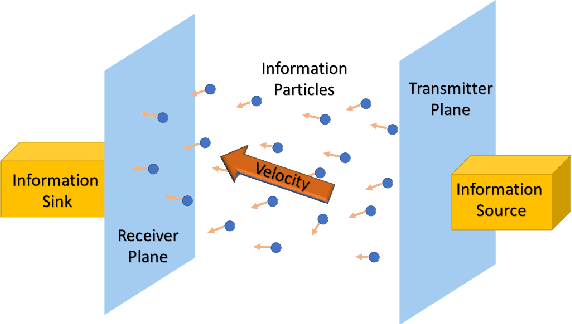
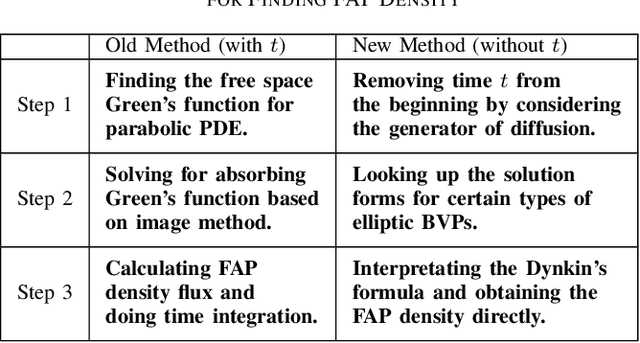
We consider the problem of characterizing the first arrival position (FAP) density in molecular communication (MC) with a diffusion-advection channel that permits a constant drift velocity pointed to arbitrary direction. The advantage of FAP modulation lies in the fact that it could encode more information into higher dimensional spatial variables, compared to other modulation techniques using time or molecule numbers. However, effective methods to characterize the FAP density in a general framework do not exist. In this paper, we devise a methodology that fully resolves the FAP density with planar absorbing receivers in arbitrary dimensions. Our work recovers existing results of FAP in 2D and 3D as special cases. The key insight of our approach is to remove the time dependence of the MC system evolution based on the generator of diffusion semigroups.