Yaya Zhanga
Dynamically configured physics-informed neural network in topology optimization applications
Dec 12, 2023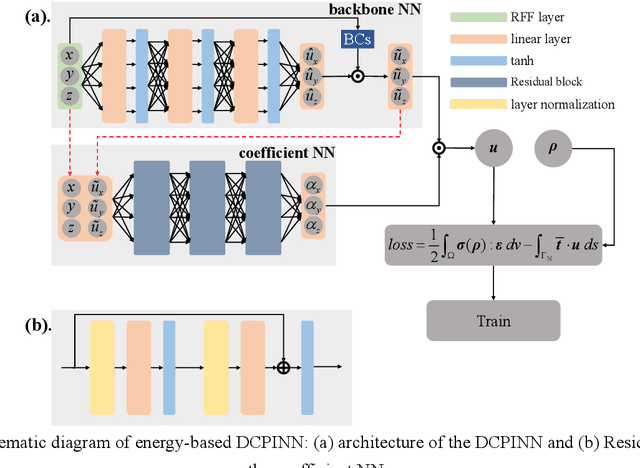
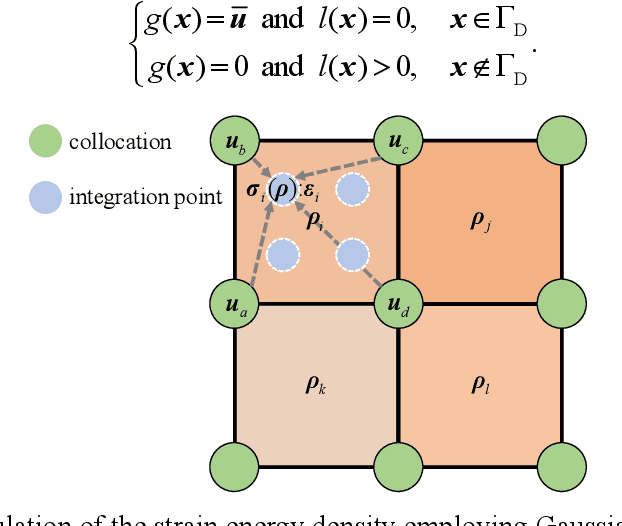
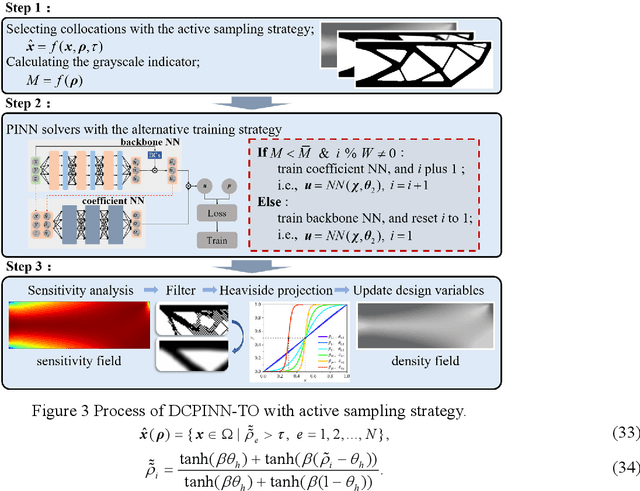
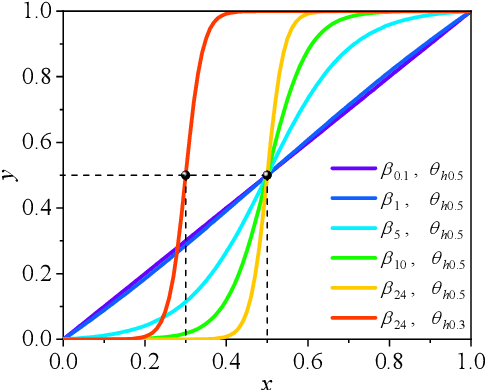
Abstract:Integration of machine learning (ML) into the topology optimization (TO) framework is attracting increasing attention, but data acquisition in data-driven models is prohibitive. Compared with popular ML methods, the physics-informed neural network (PINN) can avoid generating enormous amounts of data when solving forward problems and additionally provide better inference. To this end, a dynamically configured PINN-based topology optimization (DCPINN-TO) method is proposed. The DCPINN is composed of two subnetworks, namely the backbone neural network (NN) and the coefficient NN, where the coefficient NN has fewer trainable parameters. The designed architecture aims to dynamically configure trainable parameters; that is, an inexpensive NN is used to replace an expensive one at certain optimization cycles. Furthermore, an active sampling strategy is proposed to selectively sample collocations depending on the pseudo-densities at each optimization cycle. In this manner, the number of collocations will decrease with the optimization process but will hardly affect it. The Gaussian integral is used to calculate the strain energy of elements, which yields a byproduct of decoupling the mapping of the material at the collocations. Several examples with different resolutions validate the feasibility of the DCPINN-TO method, and multiload and multiconstraint problems are employed to illustrate its generalization. In addition, compared to finite element analysis-based TO (FEA-TO), the accuracy of the displacement prediction and optimization results indicate that the DCPINN-TO method is effective and efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge