Yasuhiko Asao
Convergence of neural networks to Gaussian mixture distribution
Apr 26, 2022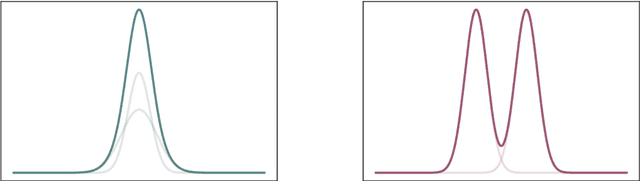
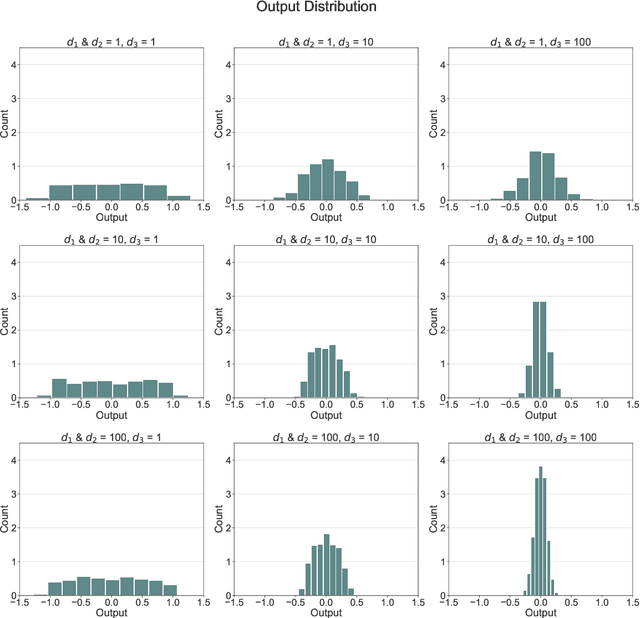
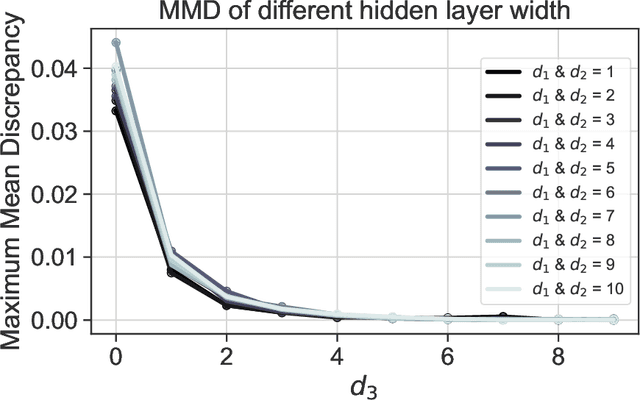
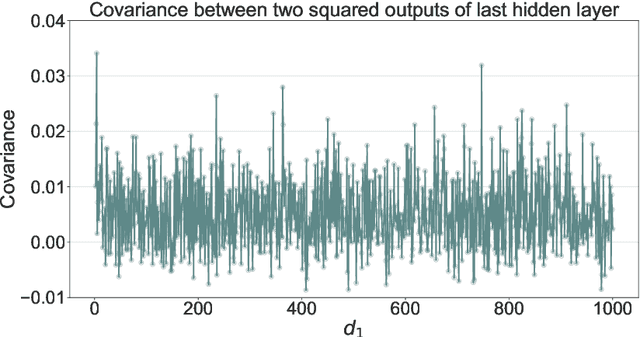
Abstract:We give a proof that, under relatively mild conditions, fully-connected feed-forward deep random neural networks converge to a Gaussian mixture distribution as only the width of the last hidden layer goes to infinity. We conducted experiments for a simple model which supports our result. Moreover, it gives a detailed description of the convergence, namely, the growth of the last hidden layer gets the distribution closer to the Gaussian mixture, and the other layer successively get the Gaussian mixture closer to the normal distribution.
Image recognition via Vietoris-Rips complex
Sep 06, 2021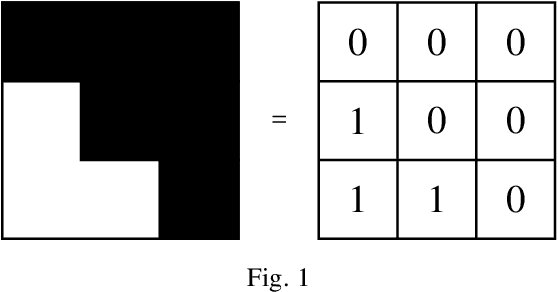
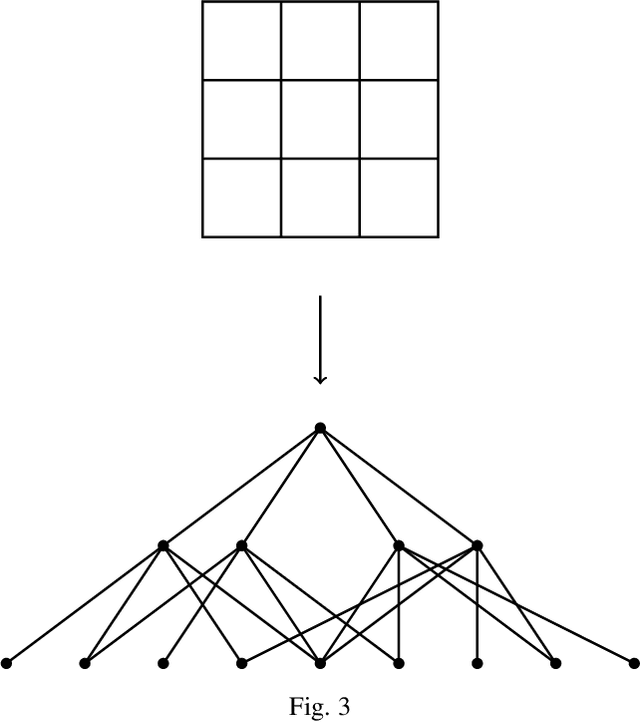
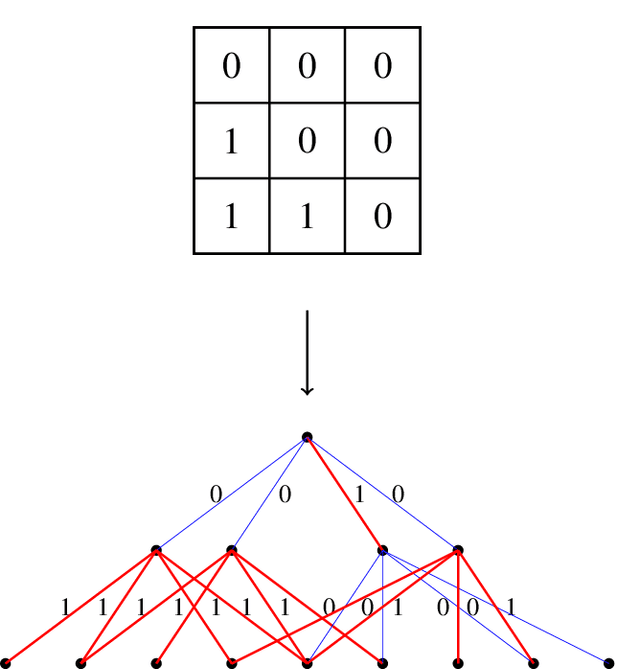
Abstract:Extracting informative features from images has been of capital importance in computer vision. In this paper, we propose a way to extract such features from images by a method based on algebraic topology. To that end, we construct a weighted graph from an image, which extracts local information of an image. By considering this weighted graph as a pseudo-metric space, we construct a Vietoris-Rips complex with a parameter $\varepsilon$ by a well-known process of algebraic topology. We can extract information of complexity of the image and can detect a sub-image with a relatively high concentration of information from this Vietoris-Rips complex. The parameter $\varepsilon$ of the Vietoris-Rips complex produces robustness to noise. We empirically show that the extracted feature captures well images' characteristics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge