Convergence of neural networks to Gaussian mixture distribution
Paper and Code
Apr 26, 2022
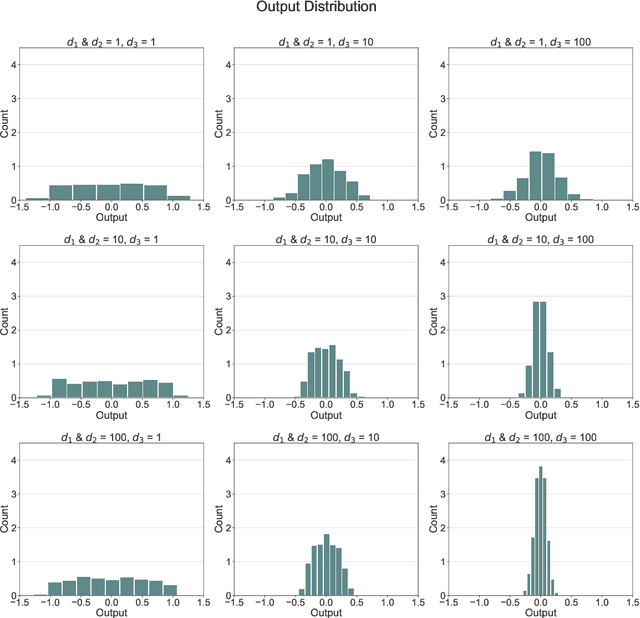
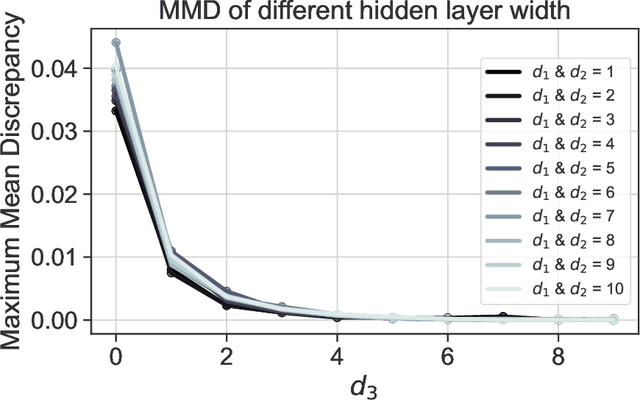
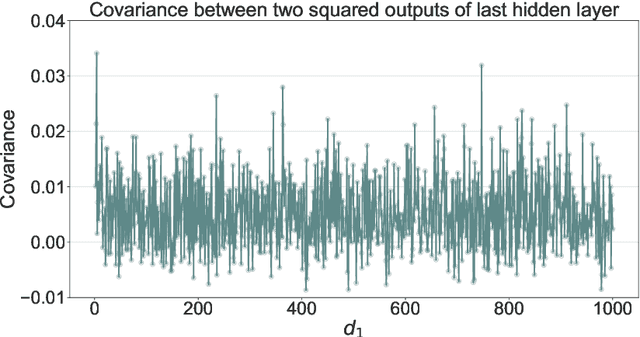
We give a proof that, under relatively mild conditions, fully-connected feed-forward deep random neural networks converge to a Gaussian mixture distribution as only the width of the last hidden layer goes to infinity. We conducted experiments for a simple model which supports our result. Moreover, it gives a detailed description of the convergence, namely, the growth of the last hidden layer gets the distribution closer to the Gaussian mixture, and the other layer successively get the Gaussian mixture closer to the normal distribution.
* 14 pages + supplemental materials
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge