Learning on Graphs for Mineral Asset Valuation Under Supply and Demand Uncertainty

Valuing mineral assets is a challenging task that is highly dependent on the supply (geological) uncertainty surrounding resources and reserves, and the uncertainty of demand (commodity prices). In this work, a graph-based reasoning, modeling and solution approach is proposed to jointly address mineral asset valuation and mine plan scheduling and optimization under supply and demand uncertainty in the "mining complex" framework. Three graph-based solutions are proposed: (i) a neural branching policy that learns a block-sampling ore body representation, (ii) a guiding policy that learns to explore a heuristic selection tree, (iii) a hyper-heuristic that manages the value/supply chain optimization and dynamics modeled as a graph structure. Results on two large-scale industrial mining complexes show a reduction of up to three orders of magnitude in primal suboptimality, execution time, and number of iterations, and an increase of up to 40% in the mineral asset value.

Learning to Schedule Heuristics for the Simultaneous Stochastic Optimization of Mining Complexes

The simultaneous stochastic optimization of mining complexes (SSOMC) is a large-scale stochastic combinatorial optimization problem that simultaneously manages the extraction of materials from multiple mines and their processing using interconnected facilities to generate a set of final products, while taking into account material supply (geological) uncertainty to manage the associated risk. Although simulated annealing has been shown to outperform comparing methods for solving the SSOMC, early performance might dominate recent performance in that a combination of the heuristics' performance is used to determine which perturbations to apply. This work proposes a data-driven framework for heuristic scheduling in a fully self-managed hyper-heuristic to solve the SSOMC. The proposed learn-to-perturb (L2P) hyper-heuristic is a multi-neighborhood simulated annealing algorithm. The L2P selects the heuristic (perturbation) to be applied in a self-adaptive manner using reinforcement learning to efficiently explore which local search is best suited for a particular search point. Several state-of-the-art agents have been incorporated into L2P to better adapt the search and guide it towards better solutions. By learning from data describing the performance of the heuristics, a problem-specific ordering of heuristics that collectively finds better solutions faster is obtained. L2P is tested on several real-world mining complexes, with an emphasis on efficiency, robustness, and generalization capacity. Results show a reduction in the number of iterations by 30-50% and in the computational time by 30-45%.

Structured Convolutional Kernel Networks for Airline Crew Scheduling

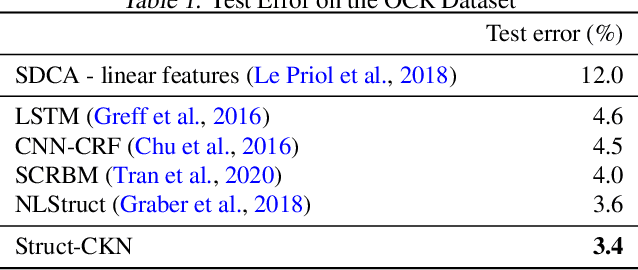
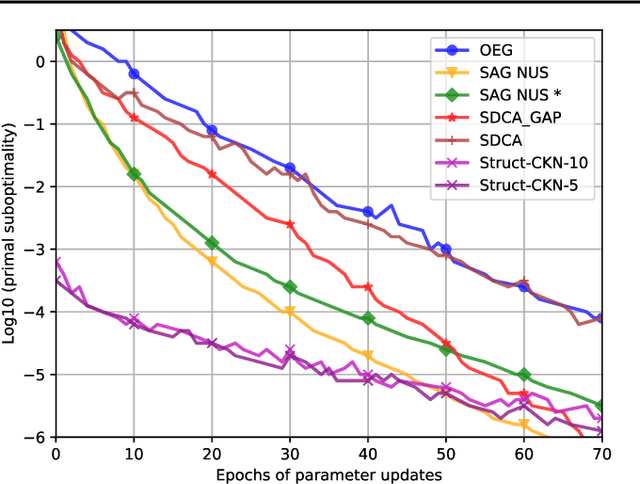
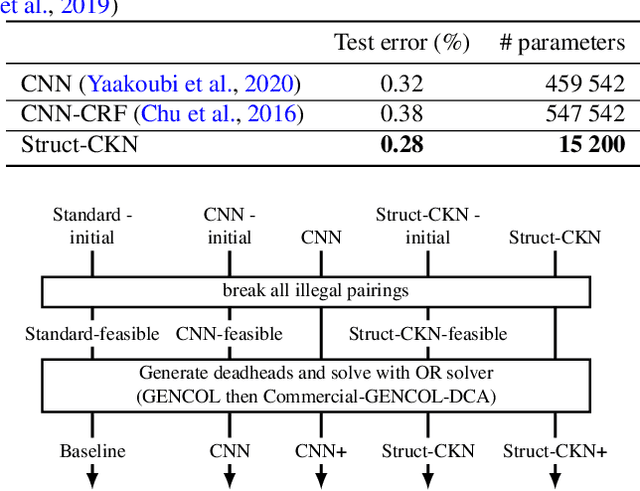
Motivated by the needs from an airline crew scheduling application, we introduce structured convolutional kernel networks (Struct-CKN), which combine CKNs from Mairal et al. (2014) in a structured prediction framework that supports constraints on the outputs. CKNs are a particular kind of convolutional neural networks that approximate a kernel feature map on training data, thus combining properties of deep learning with the non-parametric flexibility of kernel methods. Extending CKNs to structured outputs allows us to obtain useful initial solutions on a flight-connection dataset that can be further refined by an airline crew scheduling solver. More specifically, we use a flight-based network modeled as a general conditional random field capable of incorporating local constraints in the learning process. Our experiments demonstrate that this approach yields significant improvements for the large-scale crew pairing problem (50,000 flights per month) over standard approaches, reducing the solution cost by 17% (a gain of millions of dollars) and the cost of global constraints by 97%.

Machine Learning in Airline Crew Pairing to Construct Initial Clusters for Dynamic Constraint Aggregation

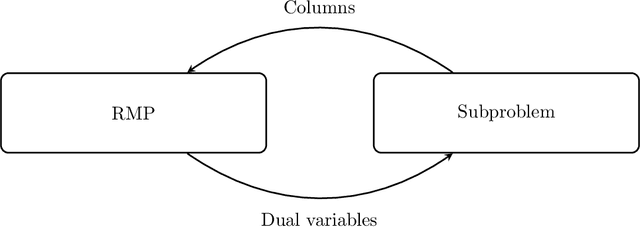
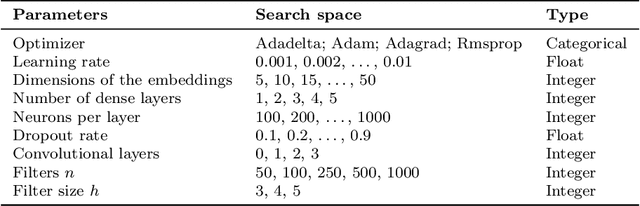
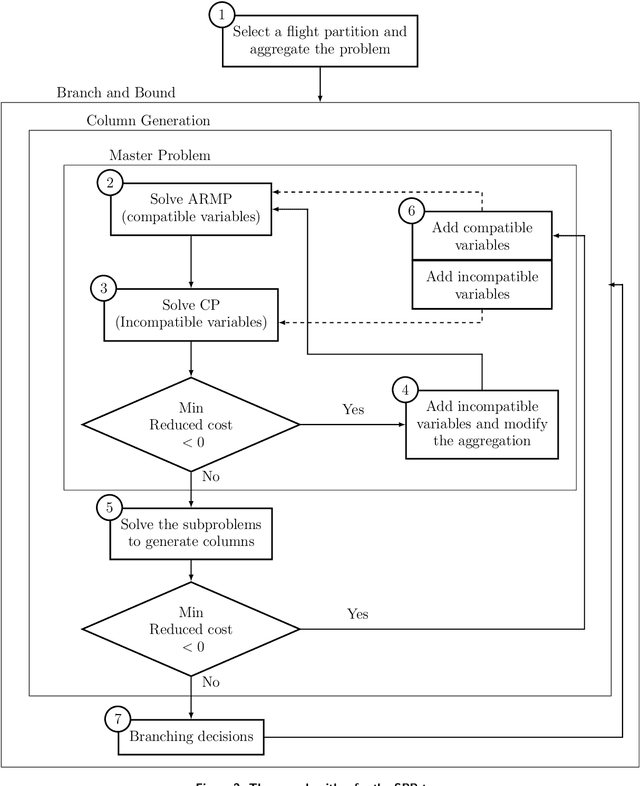
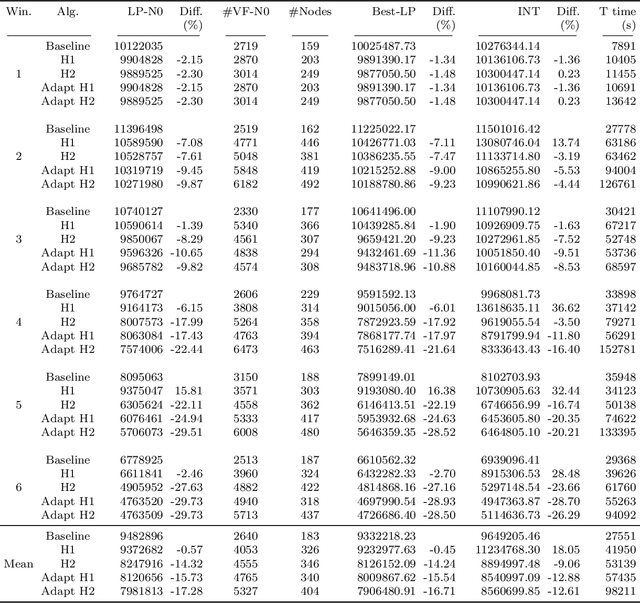
The crew pairing problem (CPP) is generally modelled as a set partitioning problem where the flights have to be partitioned in pairings. A pairing is a sequence of flight legs separated by connection time and rest periods that starts and ends at the same base. Because of the extensive list of complex rules and regulations, determining whether a sequence of flights constitutes a feasible pairing can be quite difficult by itself, making CPP one of the hardest of the airline planning problems. In this paper, we first propose to improve the prototype Baseline solver of Desaulniers et al. (2020) by adding dynamic control strategies to obtain an efficient solver for large-scale CPPs: Commercial-GENCOL-DCA. These solvers are designed to aggregate the flights covering constraints to reduce the size of the problem. Then, we use machine learning (ML) to produce clusters of flights having a high probability of being performed consecutively by the same crew. The solver combines several advanced Operations Research techniques to assemble and modify these clusters, when necessary, to produce a good solution. We show, on monthly CPPs with up to 50 000 flights, that Commercial-GENCOL-DCA with clusters produced by ML-based heuristics outperforms Baseline fed by initial clusters that are pairings of a solution obtained by rolling horizon with GENCOL. The reduction of solution cost averages between 6.8% and 8.52%, which is mainly due to the reduction in the cost of global constraints between 69.79% and 78.11%.

Flight-connection Prediction for Airline Crew Scheduling to Construct Initial Clusters for OR Optimizer

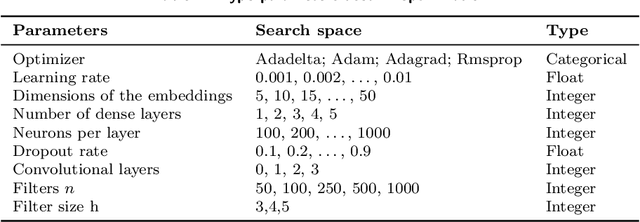
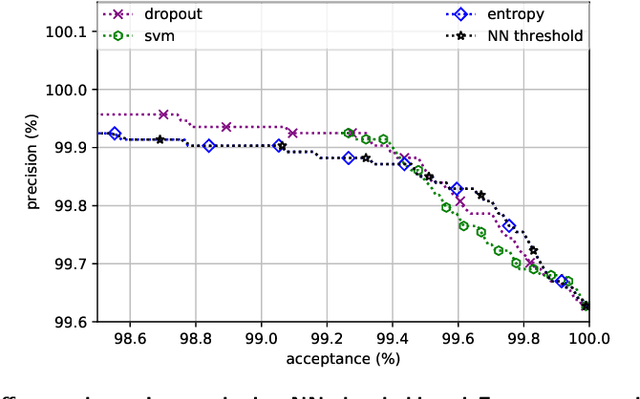
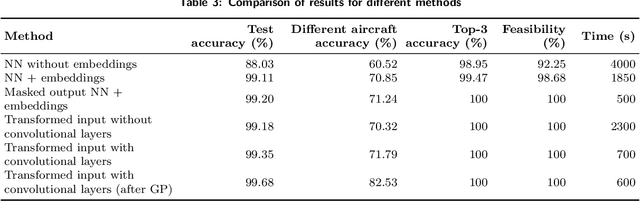
We present a case study of using machine learning classification algorithms to initialize a large scale commercial operations research solver (GENCOL) in the context of the airline crew pairing problem, where small savings of as little as 1% translate to increasing annual revenue by millions of dollars in a large airline. We focus on the problem of predicting the next connecting flight of a crew, framed as a multiclass classification problem trained from historical data, and design an adapted neural network approach that achieves high accuracy (99.7% overall or 82.5% on harder instances). We demonstrate the usefulness of our approach by using simple heuristics to combine the flight-connection predictions to form initial crew-pairing clusters that can be fed in the GENCOL solver, yielding a 10x speed improvement and up to 0.2% cost saving.