Sample-and-Bound for Non-Convex Optimization

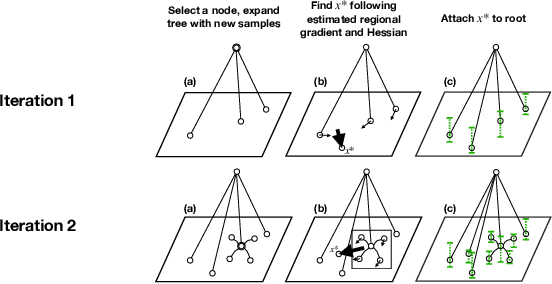
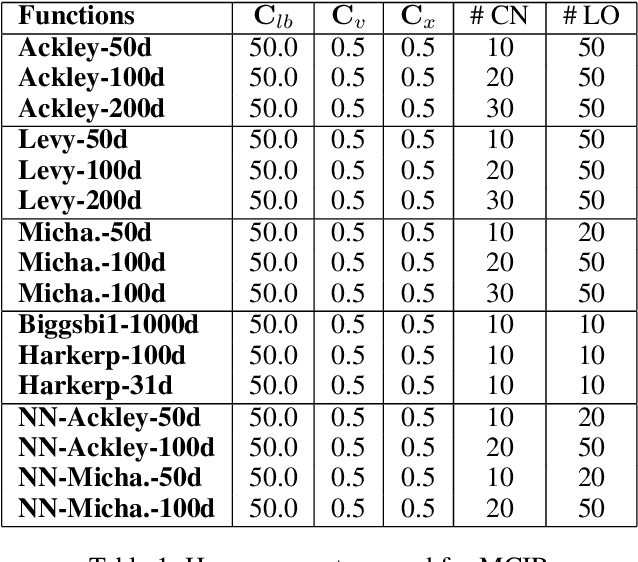
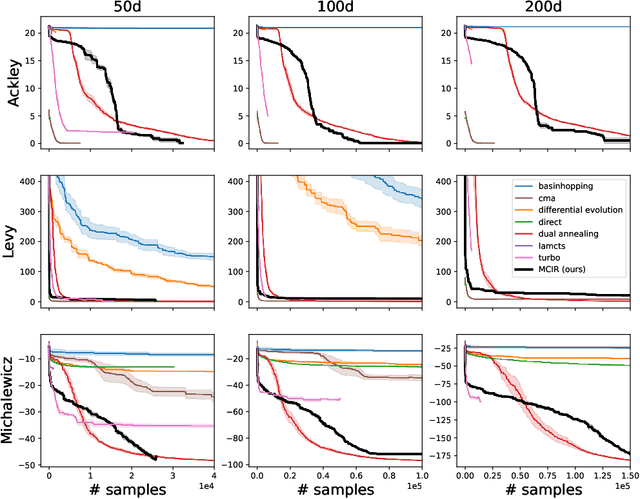
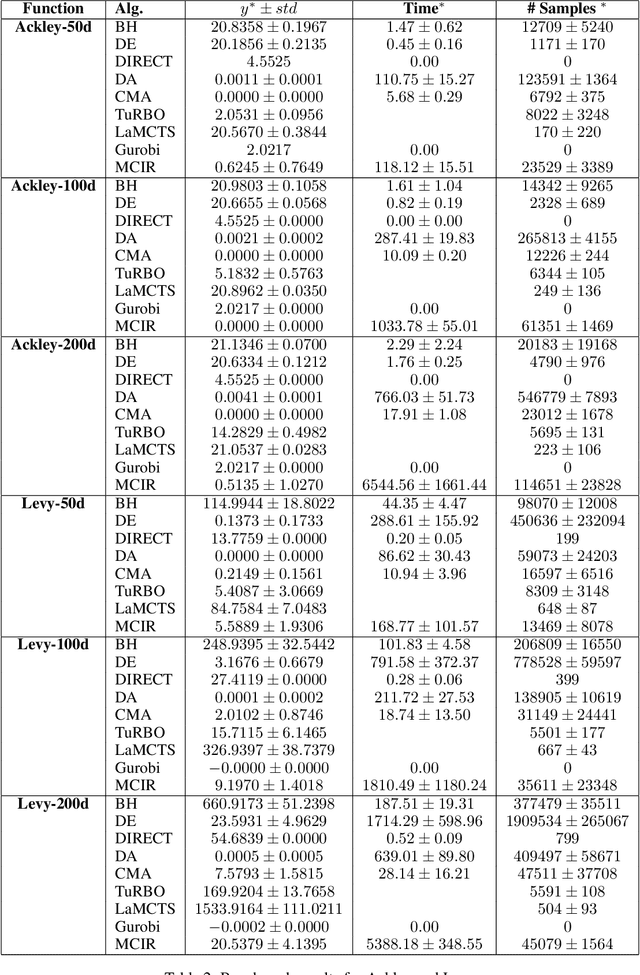
Standard approaches for global optimization of non-convex functions, such as branch-and-bound, maintain partition trees to systematically prune the domain. The tree size grows exponentially in the number of dimensions. We propose new sampling-based methods for non-convex optimization that adapts Monte Carlo Tree Search (MCTS) to improve efficiency. Instead of the standard use of visitation count in Upper Confidence Bounds, we utilize numerical overapproximations of the objective as an uncertainty metric, and also take into account of sampled estimates of first-order and second-order information. The Monte Carlo tree in our approach avoids the usual fixed combinatorial patterns in growing the tree, and aggressively zooms into the promising regions, while still balancing exploration and exploitation. We evaluate the proposed algorithms on high-dimensional non-convex optimization benchmarks against competitive baselines and analyze the effects of the hyper parameters.

Monte Carlo Tree Descent for Black-Box Optimization

The key to Black-Box Optimization is to efficiently search through input regions with potentially widely-varying numerical properties, to achieve low-regret descent and fast progress toward the optima. Monte Carlo Tree Search (MCTS) methods have recently been introduced to improve Bayesian optimization by computing better partitioning of the search space that balances exploration and exploitation. Extending this promising framework, we study how to further integrate sample-based descent for faster optimization. We design novel ways of expanding Monte Carlo search trees, with new descent methods at vertices that incorporate stochastic search and Gaussian Processes. We propose the corresponding rules for balancing progress and uncertainty, branch selection, tree expansion, and backpropagation. The designed search process puts more emphasis on sampling for faster descent and uses localized Gaussian Processes as auxiliary metrics for both exploitation and exploration. We show empirically that the proposed algorithms can outperform state-of-the-art methods on many challenging benchmark problems.