Learning low-rank latent mesoscale structures in networks

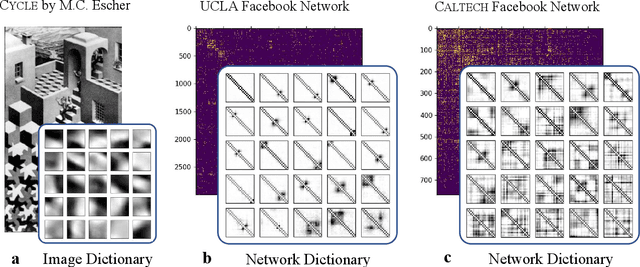
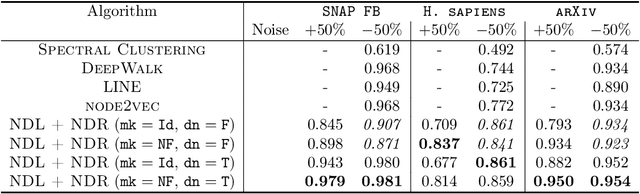
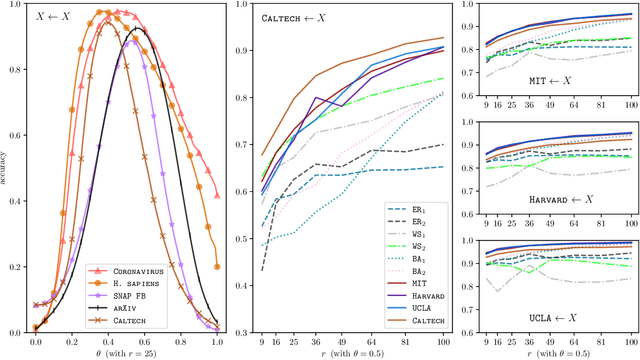
It is common to use networks to encode the architecture of interactions between entities in complex systems in the physical, biological, social, and information sciences. Moreover, to study the large-scale behavior of complex systems, it is important to study mesoscale structures in networks as building blocks that influence such behavior. In this paper, we present a new approach for describing low-rank mesoscale structure in networks, and we illustrate our approach using several synthetic network models and empirical friendship, collaboration, and protein--protein interaction (PPI) networks. We find that these networks possess a relatively small number of `latent motifs' that together can successfully approximate most subnetworks at a fixed mesoscale. We use an algorithm that we call "network dictionary learning" (NDL), which combines a network sampling method and nonnegative matrix factorization, to learn the latent motifs of a given network. The ability to encode a network using a set of latent motifs has a wide range of applications to network-analysis tasks, such as comparison, denoising, and edge inference. Additionally, using our new network denoising and reconstruction (NDR) algorithm, we demonstrate how to denoise a corrupted network by using only the latent motifs that one learns directly from the corrupted networks.