Y. SarcheshmehPour
flow-based clustering and spectral clustering: a comparison
Jun 20, 2022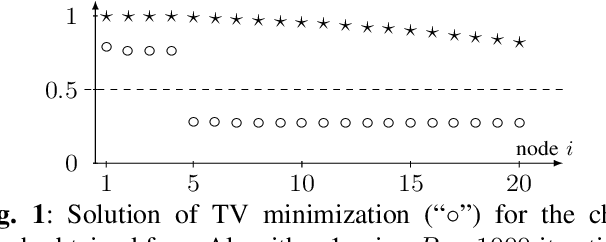
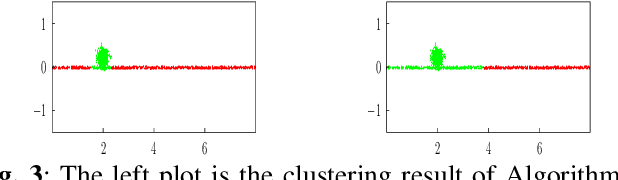

Abstract:We propose and study a novel graph clustering method for data with an intrinsic network structure. Similar to spectral clustering, we exploit an intrinsic network structure of data to construct Euclidean feature vectors. These feature vectors can then be fed into basic clustering methods such as k-means or Gaussian mixture model (GMM) based soft clustering. What sets our approach apart from spectral clustering is that we do not use the eigenvectors of a graph Laplacian to construct the feature vectors. Instead, we use the solutions of total variation minimization problems to construct feature vectors that reflect connectivity between data points. Our motivation is that the solutions of total variation minimization are piece-wise constant around a given set of seed nodes. These seed nodes can be obtained from domain knowledge or by simple heuristics that are based on the network structure of data. Our results indicate that our clustering methods can cope with certain graph structures that are challenging for spectral clustering methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge