Diffusion Boosted Trees

Combining the merits of both denoising diffusion probabilistic models and gradient boosting, the diffusion boosting paradigm is introduced for tackling supervised learning problems. We develop Diffusion Boosted Trees (DBT), which can be viewed as both a new denoising diffusion generative model parameterized by decision trees (one single tree for each diffusion timestep), and a new boosting algorithm that combines the weak learners into a strong learner of conditional distributions without making explicit parametric assumptions on their density forms. We demonstrate through experiments the advantages of DBT over deep neural network-based diffusion models as well as the competence of DBT on real-world regression tasks, and present a business application (fraud detection) of DBT for classification on tabular data with the ability of learning to defer.

CARD: Classification and Regression Diffusion Models

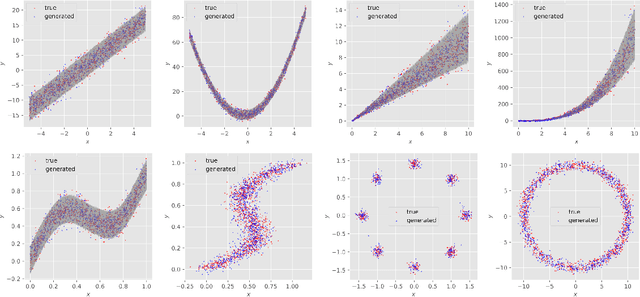
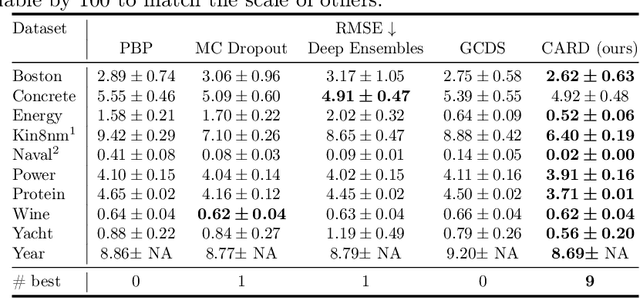
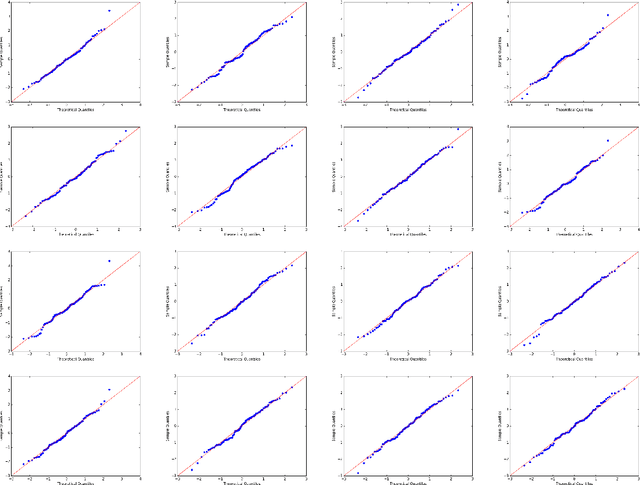
Learning the distribution of a continuous or categorical response variable $\boldsymbol y$ given its covariates $\boldsymbol x$ is a fundamental problem in statistics and machine learning. Deep neural network-based supervised learning algorithms have made great progress in predicting the mean of $\boldsymbol y$ given $\boldsymbol x$, but they are often criticized for their ability to accurately capture the uncertainty of their predictions. In this paper, we introduce classification and regression diffusion (CARD) models, which combine a denoising diffusion-based conditional generative model and a pre-trained conditional mean estimator, to accurately predict the distribution of $\boldsymbol y$ given $\boldsymbol x$. We demonstrate the outstanding ability of CARD in conditional distribution prediction with both toy examples and real-world datasets, the experimental results on which show that CARD in general outperforms state-of-the-art methods, including Bayesian neural network-based ones that are designed for uncertainty estimation, especially when the conditional distribution of $\boldsymbol y$ given $\boldsymbol x$ is multi-modal.