Physics-Informed Neural Network for Modelling the Thermochemical Curing Process of Composite-Tool Systems During Manufacture

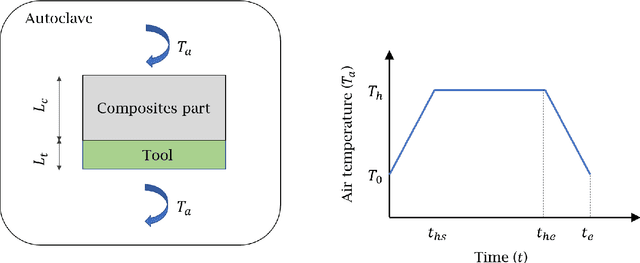
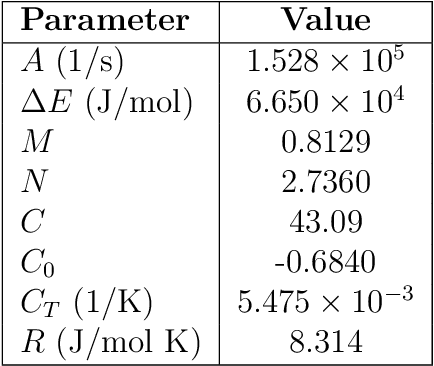
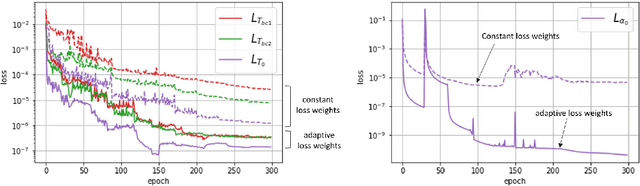
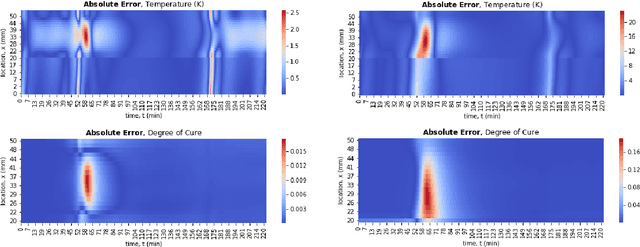
We present a Physics-Informed Neural Network (PINN) to simulate the thermochemical evolution of a composite material on a tool undergoing cure in an autoclave. In particular, we solve the governing coupled system of differential equations -- including conductive heat transfer and resin cure kinetics -- by optimizing the parameters of a deep neural network using a physics-based loss function. To account for the vastly different behaviour of thermal conduction and resin cure, we design a PINN consisting of two disconnected subnetworks, and develop a sequential training algorithm that mitigates instability present in traditional training methods. Further, we incorporate explicit discontinuities into the DNN at the composite-tool interface and enforce known physical behaviour directly in the loss function to improve the solution near the interface. Finally, we train the PINN with a technique that automatically adapts the weights on the loss terms corresponding to PDE, boundary, interface, and initial conditions. The performance of the proposed PINN is demonstrated in multiple scenarios with different material thicknesses and thermal boundary conditions.

Universal Boosting Variational Inference

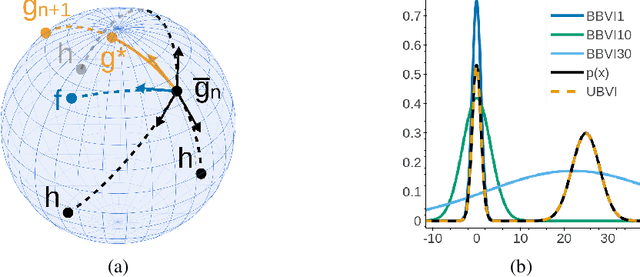
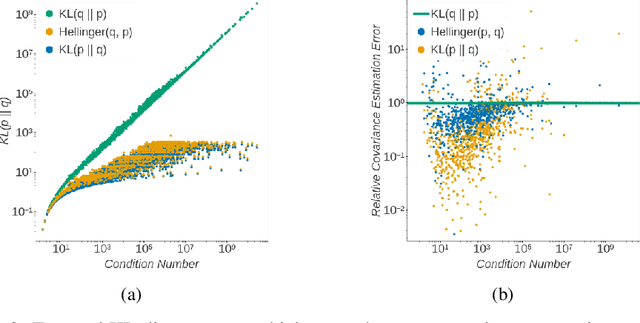
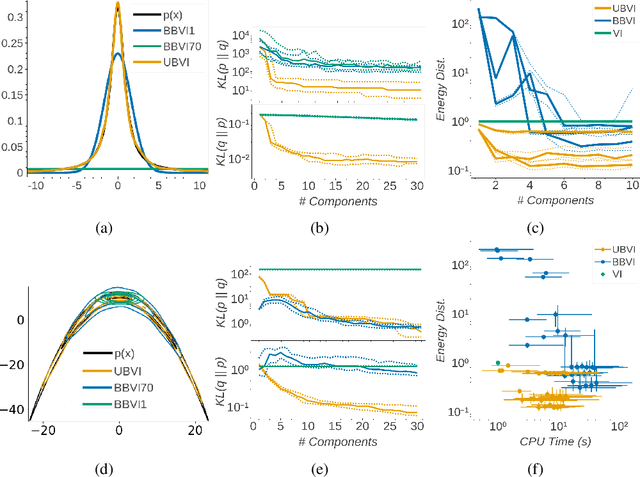
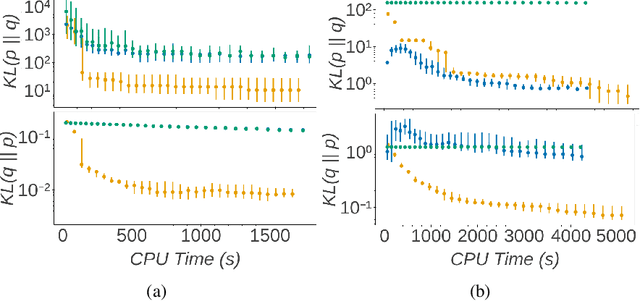
Boosting variational inference (BVI) approximates an intractable probability density by iteratively building up a mixture of simple component distributions one at a time, using techniques from sparse convex optimization to provide both computational scalability and approximation error guarantees. But the guarantees have strong conditions that do not often hold in practice, resulting in degenerate component optimization problems; and we show that the ad-hoc regularization used to prevent degeneracy in practice can cause BVI to fail in unintuitive ways. We thus develop universal boosting variational inference (UBVI), a BVI scheme that exploits the simple geometry of probability densities under the Hellinger metric to prevent the degeneracy of other gradient-based BVI methods, avoid difficult joint optimizations of both component and weight, and simplify fully-corrective weight optimizations. We show that for any target density and any mixture component family, the output of UBVI converges to the best possible approximation in the mixture family, even when the mixture family is misspecified. We develop a scalable implementation based on exponential family mixture components and standard stochastic optimization techniques. Finally, we discuss statistical benefits of the Hellinger distance as a variational objective through bounds on posterior probability, moment, and importance sampling errors. Experiments on multiple datasets and models show that UBVI provides reliable, accurate posterior approximations.