Multi-modal and frequency-weighted tensor nuclear norm for hyperspectral image denoising

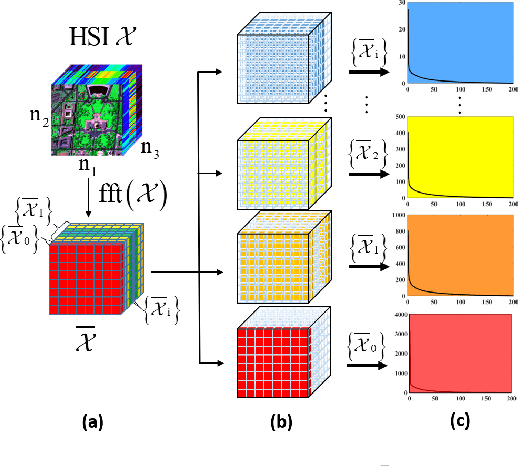
Low-rankness is important in the hyperspectral image (HSI) denoising tasks. The tensor nuclear norm (TNN), defined based on the tensor singular value decomposition, is a state-of-the-art method to describe the low-rankness of HSI. However, TNN ignores some of the physical meanings of HSI in tackling the denoising tasks, leading to suboptimal denoising performance. In this paper, we propose the multi-modal and frequency-weighted tensor nuclear norm (MFWTNN) and the non-convex MFWTNN for HSI denoising tasks. Firstly, we investigate the physical meaning of frequency components and reconsider their weights to improve the low-rank representation ability of TNN. Meanwhile, we also consider the correlation among two spatial dimensions and the spectral dimension of HSI and combine the above improvements to TNN to propose MFWTNN. Secondly, we use non-convex functions to approximate the rank function of the frequency tensor and propose the NonMFWTNN to relax the MFWTNN better. Besides, we adaptively choose bigger weights for slices mainly containing noise information and smaller weights for slices containing profile information. Finally, we develop the efficient alternating direction method of multiplier (ADMM) based algorithm to solve the proposed models, and the effectiveness of our models are substantiated in simulated and real HSI datasets.

Hyperspectral Image Restoration via Multi-mode and Double-weighted Tensor Nuclear Norm Minimization

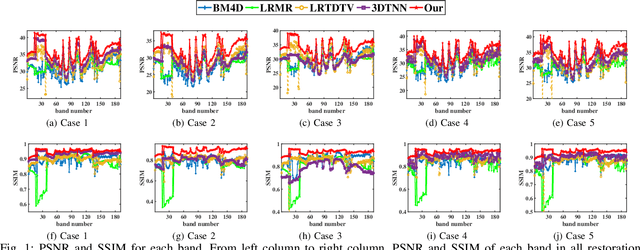
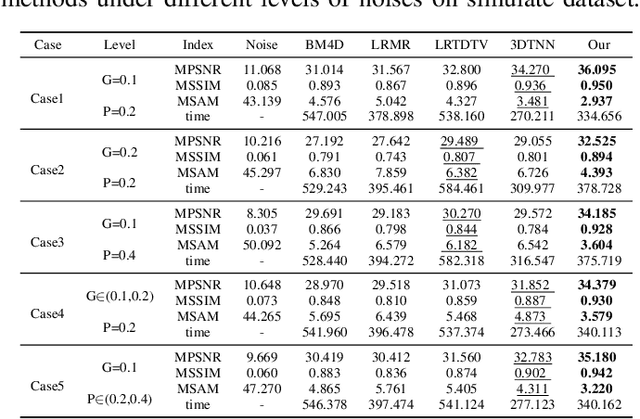
Tensor nuclear norm (TNN) induced by tensor singular value decomposition plays an important role in hyperspectral image (HSI) restoration tasks. In this letter, we first consider three inconspicuous but crucial phenomenons in TNN. In the Fourier transform domain of HSIs, different frequency components contain different information; different singular values of each frequency component also represent different information. The two physical phenomenons lie not only in the spectral dimension but also in the spatial dimensions. Then, to improve the capability and flexibility of TNN for HSI restoration, we propose a multi-mode and double-weighted TNN based on the above three crucial phenomenons. It can adaptively shrink the frequency components and singular values according to their physical meanings in all modes of HSIs. In the framework of the alternating direction method of multipliers, we design an effective alternating iterative strategy to optimize our proposed model. Restoration experiments on both synthetic and real HSI datasets demonstrate their superiority against related methods.

Enhanced nonconvex low-rank approximation of tensor multi-modes for tensor completion

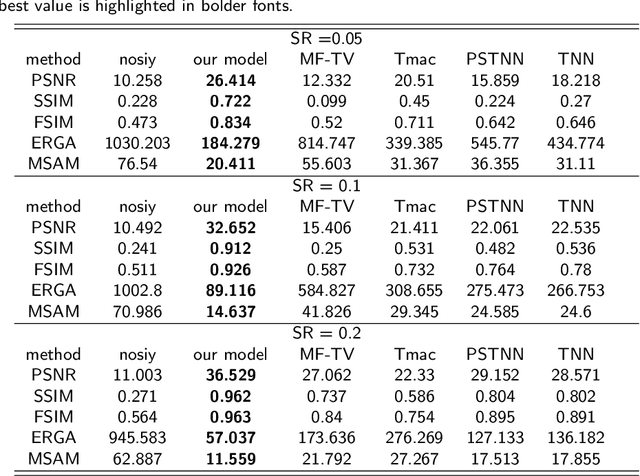
Higher-order low-rank tensor arises in many data processing applications and has attracted great interests. Inspired by low-rank approximation theory, researchers have proposed a series of effective tensor completion methods. However, most of these methods directly consider the global low-rankness of underlying tensors, which is not sufficient for a low sampling rate; in addition, the single nuclear norm or its relaxation is usually adopted to approximate the rank function, which would lead to suboptimal solution deviated from the original one. To alleviate the above problems, in this paper, we propose a novel low-rank approximation of tensor multi-modes (LRATM), in which a double nonconvex $L_{\gamma}$ norm is designed to represent the underlying joint-manifold drawn from the modal factorization factors of the underlying tensor. A block successive upper-bound minimization method-based algorithm is designed to efficiently solve the proposed model, and it can be demonstrated that our numerical scheme converges to the coordinatewise minimizers. Numerical results on three types of public multi-dimensional datasets have tested and shown that our algorithm can recover a variety of low-rank tensors with significantly fewer samples than the compared methods.

Hyperspectral Image Denoising via Global Spatial-Spectral Total Variation Regularized Nonconvex Local Low-Rank Tensor Approximation

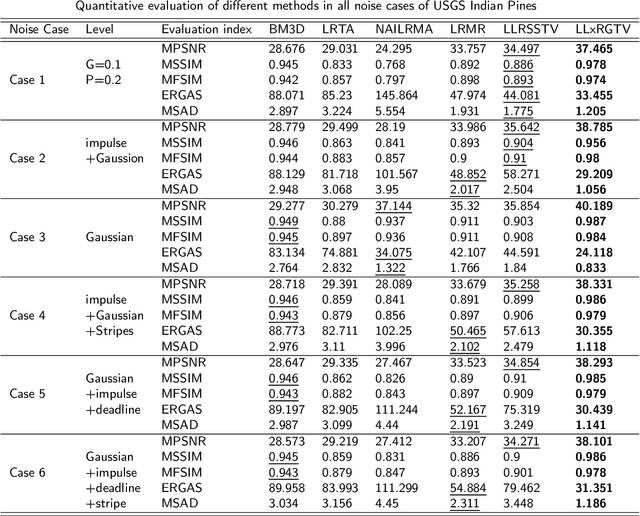
Hyperspectral image (HSI) denoising aims to restore clean HSI from the noise-contaminated one. Noise contamination can often be caused during data acquisition and conversion. In this paper, we propose a novel spatial-spectral total variation (SSTV) regularized nonconvex local low-rank (LR) tensor approximation method to remove mixed noise in HSIs. From one aspect, the clean HSI data have its underlying local LR tensor property, even though the real HSI data may not be globally low-rank due to out-liers and non-Gaussian noise. According to this fact, we propose a novel tensor $L_{\gamma}$-norm to formulate the local LR prior. From another aspect, HSIs are assumed to be piecewisely smooth in the global spatial and spectral domains. Instead of traditional bandwise total variation, we use the SSTV regularization to simultaneously consider global spatial structure and spectral correlation of neighboring bands. Results on simulated and real HSI datasets indicate that the use of local LR tensor penalty and global SSTV can boost the preserving of local details and overall structural information in HSIs.

Hyperspectral Image Restoration via Global Total Variation Regularized Local nonconvex Low-Rank matrix Approximation

Several bandwise total variation (TV) regularized low-rank (LR)-based models have been proposed to remove mixed noise in hyperspectral images (HSIs). Conventionally, the rank of LR matrix is approximated using nuclear norm (NN). The NN is defined by adding all singular values together, which is essentially a $L_1$-norm of the singular values. It results in non-negligible approximation errors and thus the resulting matrix estimator can be significantly biased. Moreover, these bandwise TV-based methods exploit the spatial information in a separate manner. To cope with these problems, we propose a spatial-spectral TV (SSTV) regularized non-convex local LR matrix approximation (NonLLRTV) method to remove mixed noise in HSIs. From one aspect, local LR of HSIs is formulated using a non-convex $L_{\gamma}$-norm, which provides a closer approximation to the matrix rank than the traditional NN. From another aspect, HSIs are assumed to be piecewisely smooth in the global spatial domain. The TV regularization is effective in preserving the smoothness and removing Gaussian noise. These facts inspire the integration of the NonLLR with TV regularization. To address the limitations of bandwise TV, we use the SSTV regularization to simultaneously consider global spatial structure and spectral correlation of neighboring bands. Experiment results indicate that the use of local non-convex penalty and global SSTV can boost the preserving of spatial piecewise smoothness and overall structural information.

Tensor completion using enhanced multiple modes low-rank prior and total variation

In this paper, we propose a novel model to recover a low-rank tensor by simultaneously performing double nuclear norm regularized low-rank matrix factorizations to the all-mode matricizations of the underlying tensor. An block successive upper-bound minimization algorithm is applied to solve the model. Subsequence convergence of our algorithm can be established, and our algorithm converges to the coordinate-wise minimizers in some mild conditions. Several experiments on three types of public data sets show that our algorithm can recover a variety of low-rank tensors from significantly fewer samples than the other testing tensor completion methods.