Hyperspectral Image Restoration via Multi-mode and Double-weighted Tensor Nuclear Norm Minimization
Paper and Code
Jan 20, 2021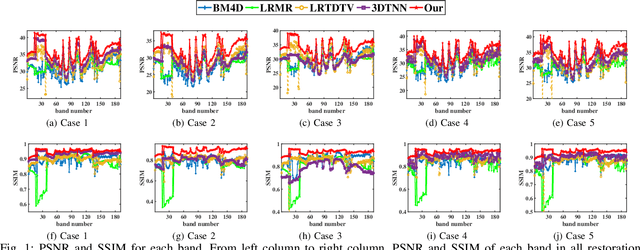

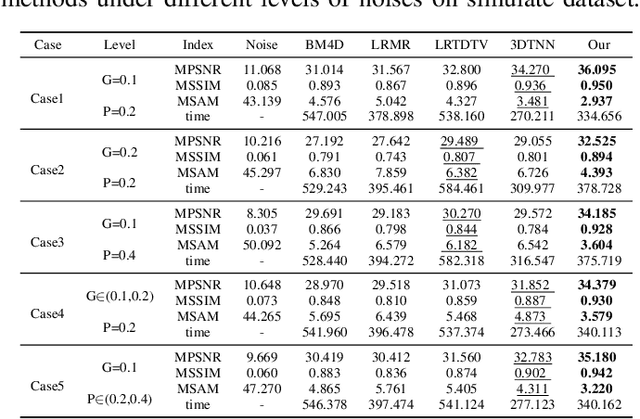
Tensor nuclear norm (TNN) induced by tensor singular value decomposition plays an important role in hyperspectral image (HSI) restoration tasks. In this letter, we first consider three inconspicuous but crucial phenomenons in TNN. In the Fourier transform domain of HSIs, different frequency components contain different information; different singular values of each frequency component also represent different information. The two physical phenomenons lie not only in the spectral dimension but also in the spatial dimensions. Then, to improve the capability and flexibility of TNN for HSI restoration, we propose a multi-mode and double-weighted TNN based on the above three crucial phenomenons. It can adaptively shrink the frequency components and singular values according to their physical meanings in all modes of HSIs. In the framework of the alternating direction method of multipliers, we design an effective alternating iterative strategy to optimize our proposed model. Restoration experiments on both synthetic and real HSI datasets demonstrate their superiority against related methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge