Element-wise Multiplication Based Physics-informed Neural Networks

As a promising framework for resolving partial differential equations (PDEs), physics-informed neural networks (PINNs) have received widespread attention from industrial and scientific fields. However, lack of expressive ability and initialization pathology issues are found to prevent the application of PINNs in complex PDEs. In this work, we propose Element-wise Multiplication Based Physics-informed Neural Networks (EM-PINNs) to resolve these issues. The element-wise multiplication operation is adopted to transform features into high-dimensional, non-linear spaces, which effectively enhance the expressive capability of PINNs. Benefiting from element-wise multiplication operation, EM-PINNs can eliminate the initialization pathologies of PINNs. The proposed structure is verified on various benchmarks. The results show that EM-PINNs have strong expressive ability.

Spatio-temporal Attention-based Hidden Physics-informed Neural Network for Remaining Useful Life Prediction

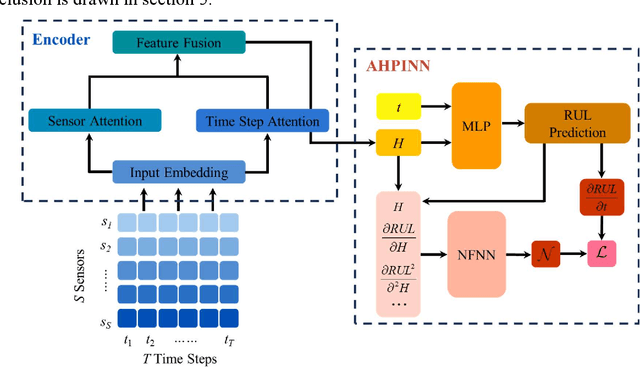
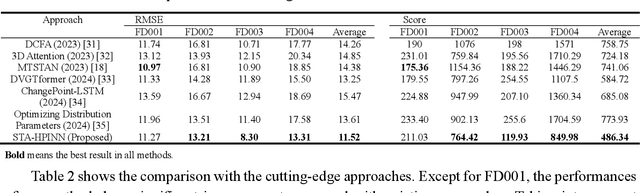
Predicting the Remaining Useful Life (RUL) is essential in Prognostic Health Management (PHM) for industrial systems. Although deep learning approaches have achieved considerable success in predicting RUL, challenges such as low prediction accuracy and interpretability pose significant challenges, hindering their practical implementation. In this work, we introduce a Spatio-temporal Attention-based Hidden Physics-informed Neural Network (STA-HPINN) for RUL prediction, which can utilize the associated physics of the system degradation. The spatio-temporal attention mechanism can extract important features from the input data. With the self-attention mechanism on both the sensor dimension and time step dimension, the proposed model can effectively extract degradation information. The hidden physics-informed neural network is utilized to capture the physics mechanisms that govern the evolution of RUL. With the constraint of physics, the model can achieve higher accuracy and reasonable predictions. The approach is validated on a benchmark dataset, demonstrating exceptional performance when compared to cutting-edge methods, especially in the case of complex conditions.

Densely Multiplied Physics Informed Neural Networks

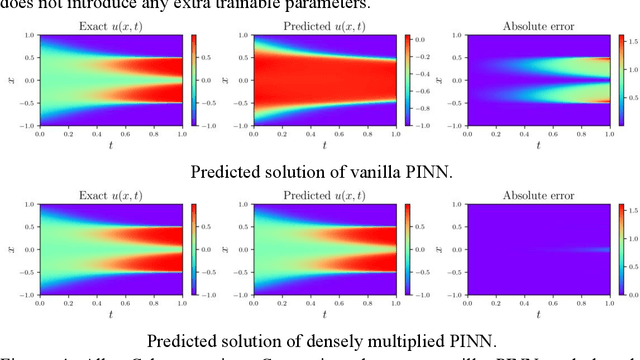
Although physics-informed neural networks (PINNs) have shown great potential in dealing with nonlinear partial differential equations (PDEs), it is common that PINNs will suffer from the problem of insufficient precision or obtaining incorrect outcomes. Unlike most of the existing solutions trying to enhance the ability of PINN by optimizing the training process, this paper improved the neural network architecture to improve the performance of PINN. We propose a densely multiply PINN (DM-PINN) architecture, which multiplies the output of a hidden layer with the outputs of all the behind hidden layers. Without introducing more trainable parameters, this effective mechanism can significantly improve the accuracy of PINNs. The proposed architecture is evaluated on four benchmark examples (Allan-Cahn equation, Helmholtz equation, Burgers equation and 1D convection equation). Comparisons between the proposed architecture and different PINN structures demonstrate the superior performance of the DM-PINN in both accuracy and efficiency.