Element-wise Multiplication Based Physics-informed Neural Networks
Paper and Code
Jun 06, 2024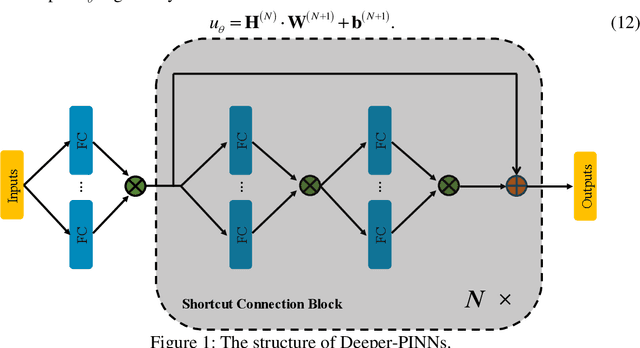
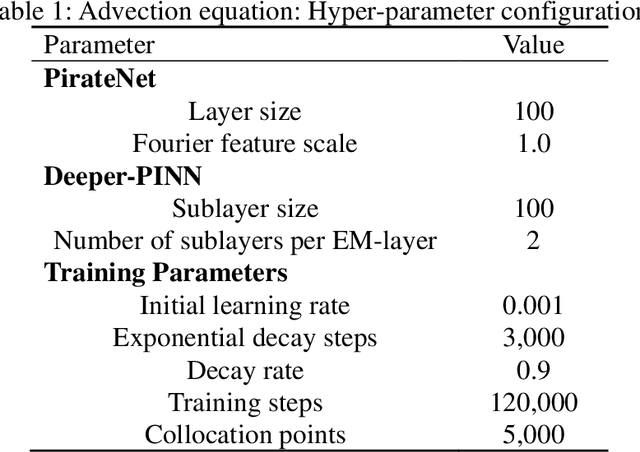
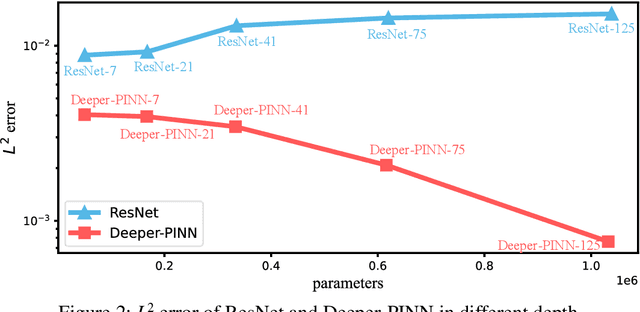
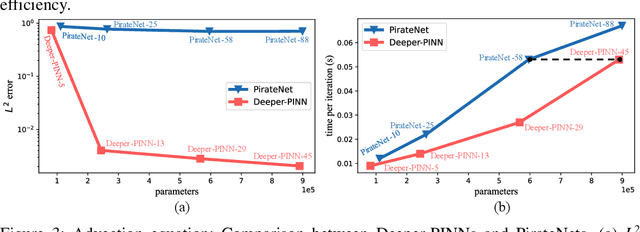
As a promising framework for resolving partial differential equations (PDEs), physics-informed neural networks (PINNs) have received widespread attention from industrial and scientific fields. However, lack of expressive ability and initialization pathology issues are found to prevent the application of PINNs in complex PDEs. In this work, we propose Element-wise Multiplication Based Physics-informed Neural Networks (EM-PINNs) to resolve these issues. The element-wise multiplication operation is adopted to transform features into high-dimensional, non-linear spaces, which effectively enhance the expressive capability of PINNs. Benefiting from element-wise multiplication operation, EM-PINNs can eliminate the initialization pathologies of PINNs. The proposed structure is verified on various benchmarks. The results show that EM-PINNs have strong expressive ability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge