Nonparametric active learning for cost-sensitive classification

Cost-sensitive learning is a common type of machine learning problem where different errors of prediction incur different costs. In this paper, we design a generic nonparametric active learning algorithm for cost-sensitive classification. Based on the construction of confidence bounds for the expected prediction cost functions of each label, our algorithm sequentially selects the most informative vector points. Then it interacts with them by only querying the costs of prediction that could be the smallest. We prove that our algorithm attains optimal rate of convergence in terms of the number of interactions with the feature vector space. Furthermore, in terms of a general version of Tsybakov's noise assumption, the gain over the corresponding passive learning is explicitly characterized by the probability-mass of the boundary decision. Additionally, we prove the near-optimality of obtained upper bounds by providing matching (up to logarithmic factor) lower bounds.

Nonparametric adaptive active learning under local smoothness condition

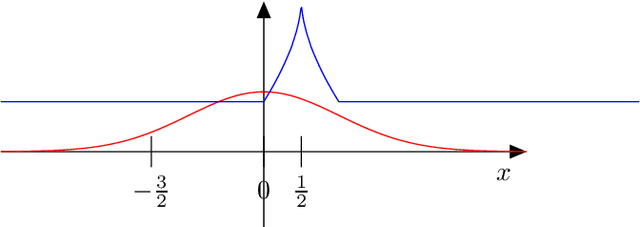
Active learning is typically used to label data, when the labeling process is expensive. Several active learning algorithms have been theoretically proved to perform better than their passive counterpart. However, these algorithms rely on some assumptions, which themselves contain some specific parameters. This paper adresses the problem of adaptive active learning in a nonparametric setting with minimal assumptions. We present a novel algorithm that is valid under more general assumptions than the previously known algorithms, and that can moreover adapt to the parameters used in these assumptions. This allows us to work with a larger class of distributions, thereby avoiding to exclude important densities like gaussians. Our algorithm achieves a minimax rate of convergence, and therefore performs almost as well as the best known non-adaptive algorithms.

Deep matrix factorizations

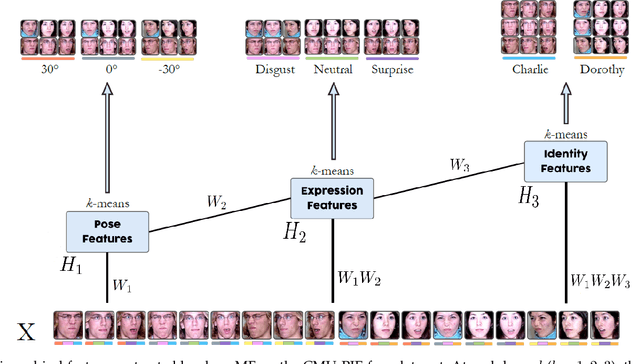
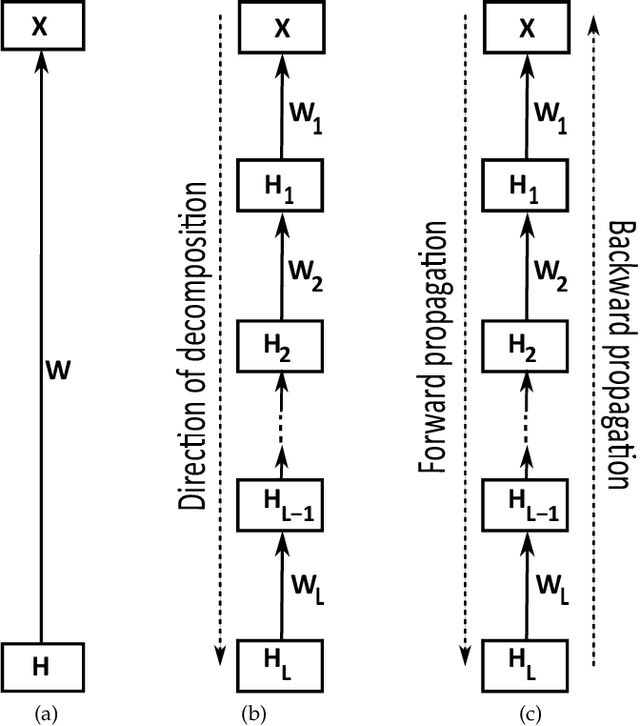
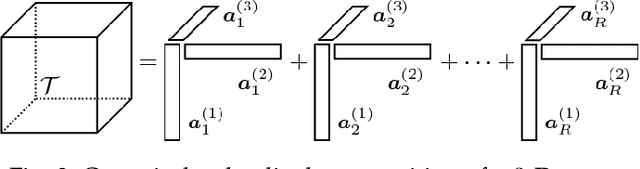
Constrained low-rank matrix approximations have been known for decades as powerful linear dimensionality reduction techniques to be able to extract the information contained in large data sets in a relevant way. However, such low-rank approaches are unable to mine complex, interleaved features that underlie hierarchical semantics. Recently, deep matrix factorization (deep MF) was introduced to deal with the extraction of several layers of features and has been shown to reach outstanding performances on unsupervised tasks. Deep MF was motivated by the success of deep learning, as it is conceptually close to some neural networks paradigms. In this paper, we present the main models, algorithms, and applications of deep MF through a comprehensive literature review. We also discuss theoretical questions and perspectives of research.

K-NN active learning under local smoothness assumption

There is a large body of work on convergence rates either in passive or active learning. Here we first outline some of the main results that have been obtained, more specifically in a nonparametric setting under assumptions about the smoothness of the regression function (or the boundary between classes) and the margin noise. We discuss the relative merits of these underlying assumptions by putting active learning in perspective with recent work on passive learning. We design an active learning algorithm with a rate of convergence better than in passive learning, using a particular smoothness assumption customized for k-nearest neighbors. Unlike previous active learning algorithms, we use a smoothness assumption that provides a dependence on the marginal distribution of the instance space. Additionally, our algorithm avoids the strong density assumption that supposes the existence of the density function of the marginal distribution of the instance space and is therefore more generally applicable.

Near-Convex Archetypal Analysis

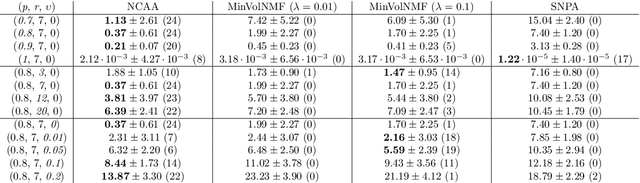
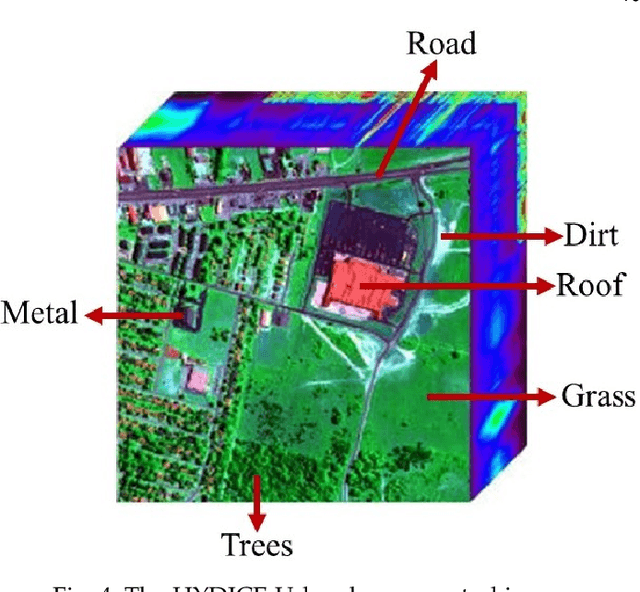
Nonnegative matrix factorization (NMF) is a widely used linear dimensionality reduction technique for nonnegative data. NMF requires that each data point is approximated by a convex combination of basis elements. Archetypal analysis (AA), also referred to as convex NMF, is a well-known NMF variant imposing that the basis elements are themselves convex combinations of the data points. AA has the advantage to be more interpretable than NMF because the basis elements are directly constructed from the data points. However, it usually suffers from a high data fitting error because the basis elements are constrained to be contained in the convex cone of the data points. In this letter, we introduce near-convex archetypal analysis (NCAA) which combines the advantages of both AA and NMF. As for AA, the basis vectors are required to be linear combinations of the data points and hence are easily interpretable. As for NMF, the additional flexibility in choosing the basis elements allows NCAA to have a low data fitting error. We show that NCAA compares favorably with a state-of-the-art minimum-volume NMF method on synthetic datasets and on a real-world hyperspectral image.

K-nn active learning under local smoothness condition

There is a large body of work on convergence rates either in passive or active learning. Here we outline some of the results that have been obtained, more specifically in a nonparametric setting under assumptions about the smoothness and the margin noise. We also discuss the relative merits of these underlying assumptions by putting active learning in perspective with recent work on passive learning. We provide a novel active learning algorithm with a rate of convergence better than in passive learning, using a particular smoothness assumption customized for $k$-nearest neighbors. This smoothness assumption provides a dependence on the marginal distribution of the instance space unlike other recent algorithms. Our algorithm thus avoids the strong density assumption that supposes the existence of the density function of the marginal distribution of the instance space and is therefore more generally applicable.