A consistent and flexible framework for deep matrix factorizations

Deep matrix factorizations (deep MFs) are recent unsupervised data mining techniques inspired by constrained low-rank approximations. They aim to extract complex hierarchies of features within high-dimensional datasets. Most of the loss functions proposed in the literature to evaluate the quality of deep MF models and the underlying optimization frameworks are not consistent because different losses are used at different layers. In this paper, we introduce two meaningful loss functions for deep MF and present a generic framework to solve the corresponding optimization problems. We illustrate the effectiveness of this approach through the integration of various constraints and regularizations, such as sparsity, nonnegativity and minimum-volume. The models are successfully applied on both synthetic and real data, namely for hyperspectral unmixing and extraction of facial features.

Deep matrix factorizations

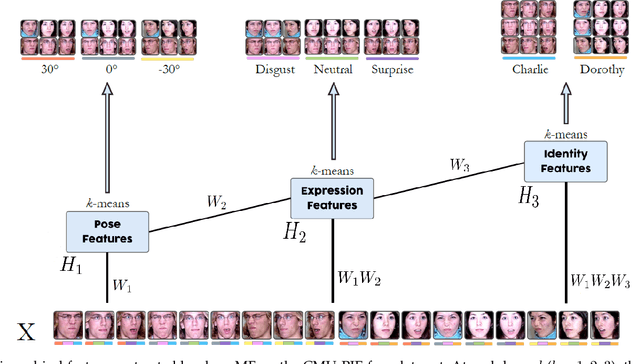
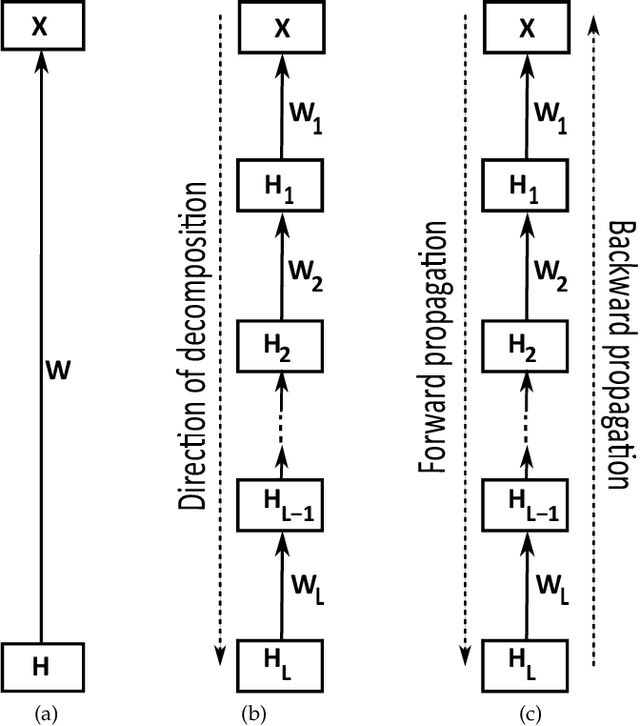
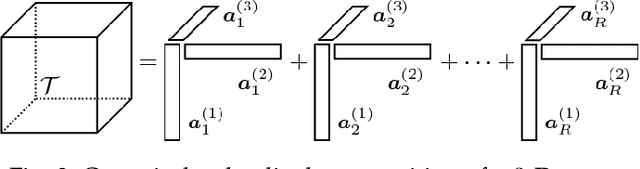
Constrained low-rank matrix approximations have been known for decades as powerful linear dimensionality reduction techniques to be able to extract the information contained in large data sets in a relevant way. However, such low-rank approaches are unable to mine complex, interleaved features that underlie hierarchical semantics. Recently, deep matrix factorization (deep MF) was introduced to deal with the extraction of several layers of features and has been shown to reach outstanding performances on unsupervised tasks. Deep MF was motivated by the success of deep learning, as it is conceptually close to some neural networks paradigms. In this paper, we present the main models, algorithms, and applications of deep MF through a comprehensive literature review. We also discuss theoretical questions and perspectives of research.

Near-Convex Archetypal Analysis

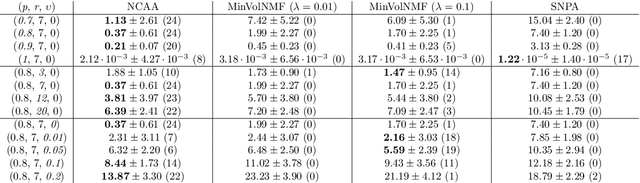
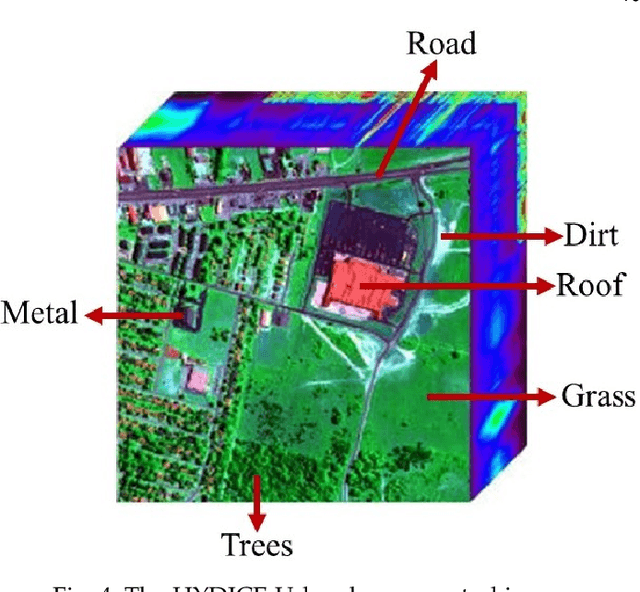
Nonnegative matrix factorization (NMF) is a widely used linear dimensionality reduction technique for nonnegative data. NMF requires that each data point is approximated by a convex combination of basis elements. Archetypal analysis (AA), also referred to as convex NMF, is a well-known NMF variant imposing that the basis elements are themselves convex combinations of the data points. AA has the advantage to be more interpretable than NMF because the basis elements are directly constructed from the data points. However, it usually suffers from a high data fitting error because the basis elements are constrained to be contained in the convex cone of the data points. In this letter, we introduce near-convex archetypal analysis (NCAA) which combines the advantages of both AA and NMF. As for AA, the basis vectors are required to be linear combinations of the data points and hence are easily interpretable. As for NMF, the additional flexibility in choosing the basis elements allows NCAA to have a low data fitting error. We show that NCAA compares favorably with a state-of-the-art minimum-volume NMF method on synthetic datasets and on a real-world hyperspectral image.