Xavier Duquesne
Congestion control algorithms for robotic swarms with a common target based on the throughput of the target area
Jan 25, 2022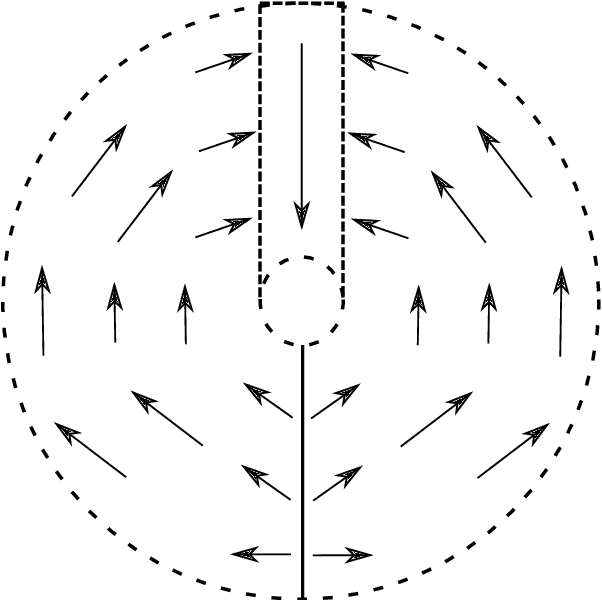

Abstract:When a large number of robots try to reach a common area, congestions happen, causing severe delays. To minimise congestion in a robotic swarm system, traffic control algorithms must be employed in a decentralised manner. Based on strategies aimed to maximise the throughput of the common target area, we developed two novel algorithms for robots using artificial potential fields for obstacle avoidance and navigation. One algorithm is inspired by creating a queue to get to the target area (Single Queue Former -- SQF), while the other makes the robots touch the boundary of the circular area by using vector fields (Touch and Run Vector Fields -- TRVF). We performed simulation experiments to show that the proposed algorithms are bounded by the throughput of their inspired theoretical strategies and compare the two novel algorithms with state-of-art algorithms for the same problem (PCC, EE and PCC-EE). The SQF algorithm significantly outperforms all other algorithms for a large number of robots or when the circular target region radius is small. TRVF, on the other hand, is better than SQF only for a limited number of robots and outperforms only PCC for numerous robots. However, it allows us to analyse the potential impacts on the throughput when transferring an idea from a theoretical strategy to a concrete algorithm that considers changing velocities and distances between robots.
On the throughput of the common target area for robotic swarm strategies -- extended version
Jan 25, 2022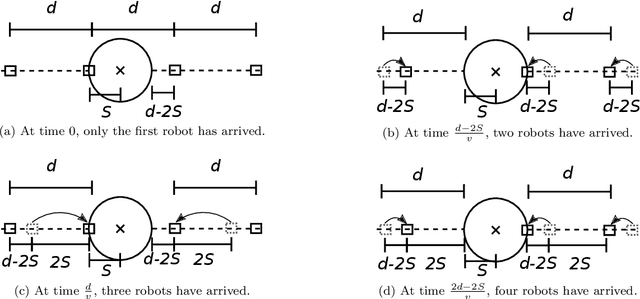
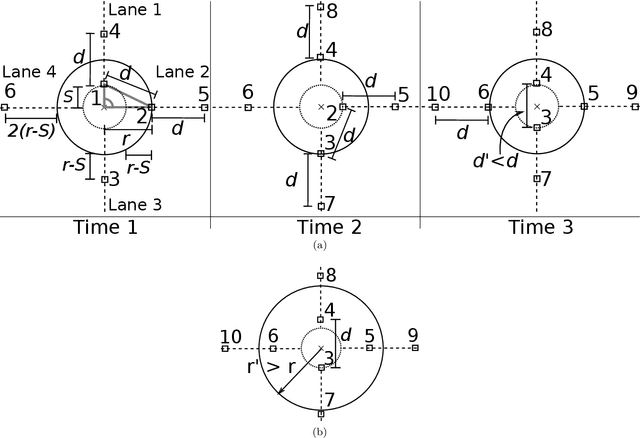
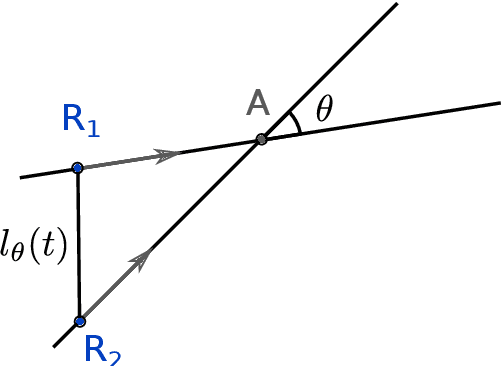
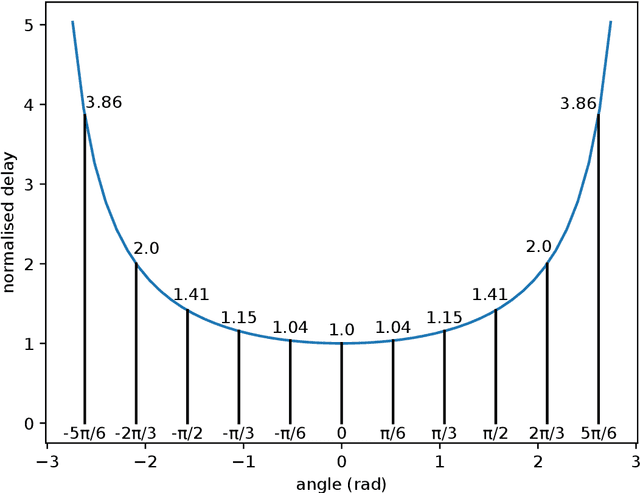
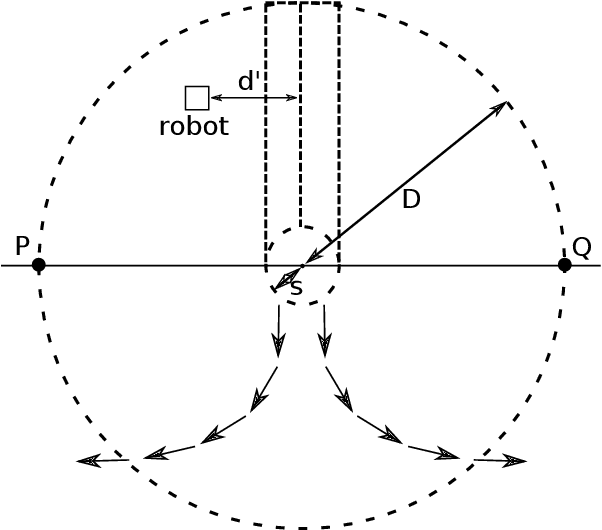
Abstract:A robotic swarm may encounter traffic congestion when many robots simultaneously attempt to reach the same area. For solving that efficiently, robots must execute decentralised traffic control algorithms. In this work, we propose a measure for evaluating the access efficiency of a common target area as the number of robots in the swarm rises: the common target area throughput. We demonstrate that the throughput of a target region with a limited area as the time tends to infinity -- the asymptotic throughput -- is finite, opposed to the relation arrival time at target per number of robots that tends to infinity. Using this measure, we can analytically compare the effectiveness of different algorithms. In particular, we propose and formally evaluate three different theoretical strategies for getting to a circular target area: (i) forming parallel queues towards the target area, (ii) forming a hexagonal packing through a corridor going to the target, and (iii) making multiple curved trajectories towards the boundary of the target area. We calculate the throughput for a fixed time and the asymptotic throughput for these strategies. Additionally, we corroborate these results by simulations, showing that when an algorithm has higher throughput, its arrival time per number of robots is lower. Thus, we conclude that using throughput is well suited for comparing congestion algorithms for a common target area in robotic swarms even if we do not have their closed asymptotic equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge