On the throughput of the common target area for robotic swarm strategies -- extended version
Paper and Code
Jan 25, 2022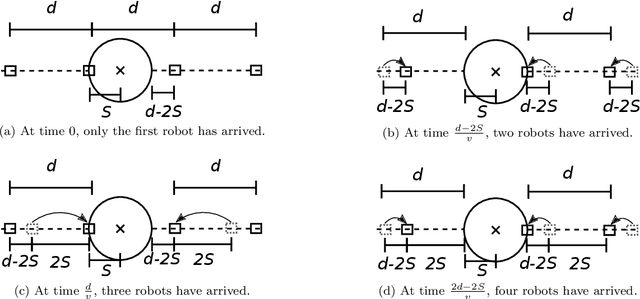
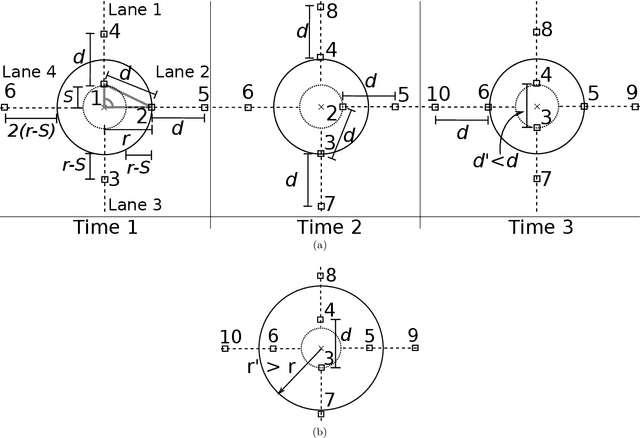
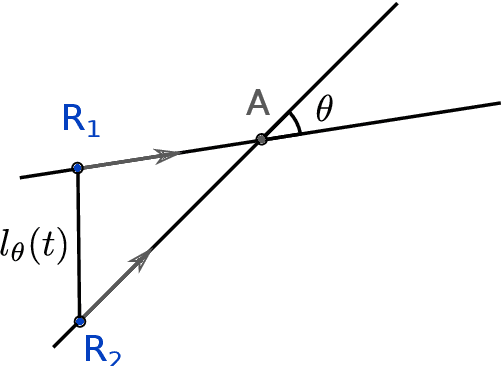
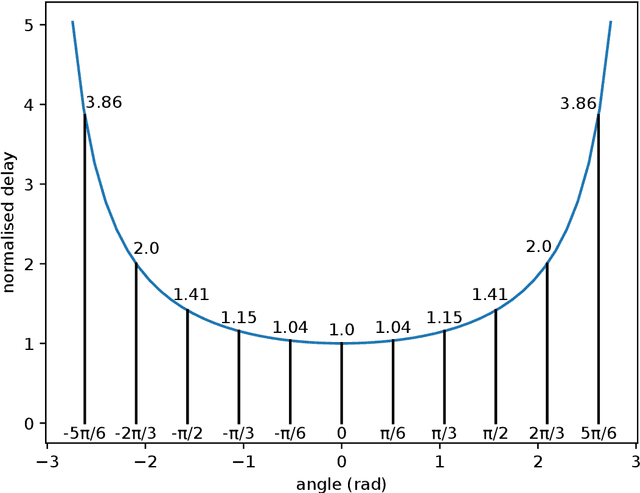
A robotic swarm may encounter traffic congestion when many robots simultaneously attempt to reach the same area. For solving that efficiently, robots must execute decentralised traffic control algorithms. In this work, we propose a measure for evaluating the access efficiency of a common target area as the number of robots in the swarm rises: the common target area throughput. We demonstrate that the throughput of a target region with a limited area as the time tends to infinity -- the asymptotic throughput -- is finite, opposed to the relation arrival time at target per number of robots that tends to infinity. Using this measure, we can analytically compare the effectiveness of different algorithms. In particular, we propose and formally evaluate three different theoretical strategies for getting to a circular target area: (i) forming parallel queues towards the target area, (ii) forming a hexagonal packing through a corridor going to the target, and (iii) making multiple curved trajectories towards the boundary of the target area. We calculate the throughput for a fixed time and the asymptotic throughput for these strategies. Additionally, we corroborate these results by simulations, showing that when an algorithm has higher throughput, its arrival time per number of robots is lower. Thus, we conclude that using throughput is well suited for comparing congestion algorithms for a common target area in robotic swarms even if we do not have their closed asymptotic equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge