Quantitative causality, causality-guided scientific discovery, and causal machine learning

It has been said, arguably, that causality analysis should pave a promising way to interpretable deep learning and generalization. Incorporation of causality into artificial intelligence (AI) algorithms, however, is challenged with its vagueness, non-quantitiveness, computational inefficiency, etc. During the past 18 years, these challenges have been essentially resolved, with the establishment of a rigorous formalism of causality analysis initially motivated from atmospheric predictability. This not only opens a new field in the atmosphere-ocean science, namely, information flow, but also has led to scientific discoveries in other disciplines, such as quantum mechanics, neuroscience, financial economics, etc., through various applications. This note provides a brief review of the decade-long effort, including a list of major theoretical results, a sketch of the causal deep learning framework, and some representative real-world applications in geoscience pertaining to this journal, such as those on the anthropogenic cause of global warming, the decadal prediction of El Ni\~no Modoki, the forecasting of an extreme drought in China, among others.

An overview of the quantitative causality analysis and causal graph reconstruction based on a rigorous formalism of information flow

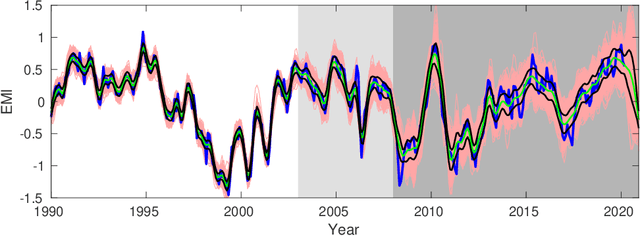
Inference of causal relations from data now has become an important field in artificial intelligence. During the past 16 years, causality analysis (in a quantitative sense) has been developed independently in physics from first principles. This short note is a brief summary of this line of work, including part of the theory and several representative applications.

Normalized multivariate time series causality analysis and causal graph reconstruction

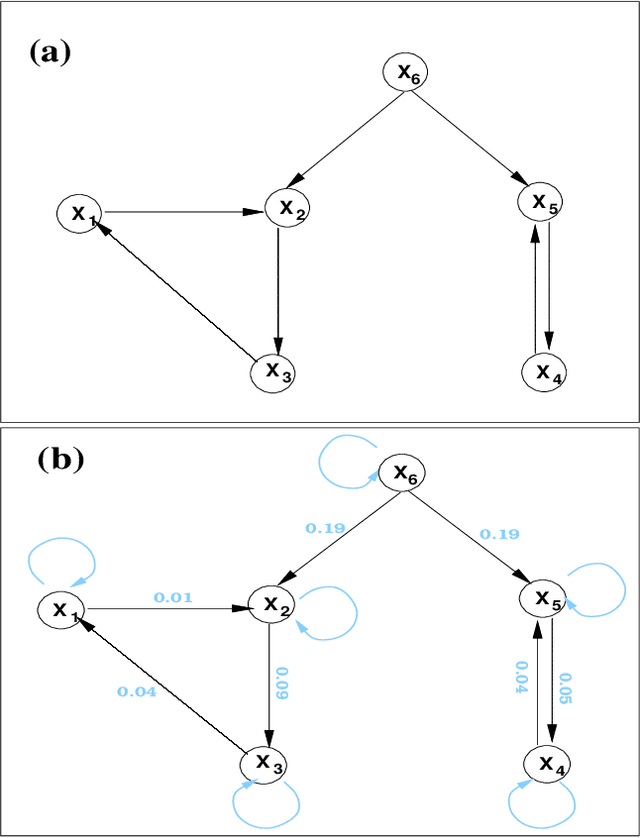
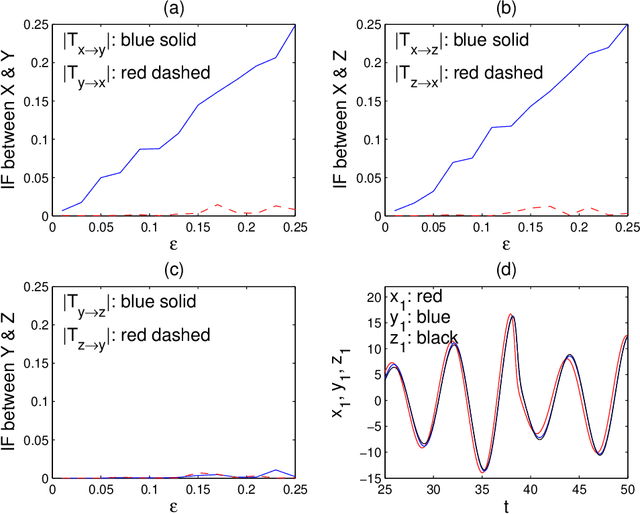
Causality analysis is an important problem lying at the heart of science, and is of particular importance in data science and machine learning. An endeavor during the past 16 years viewing causality as real physical notion so as to formulate it from first principles, however, seems to go unnoticed. This study introduces to the community this line of work, with a long-due generalization of the information flow-based bivariate time series causal inference to multivariate series, based on the recent advance in theoretical development. The resulting formula is transparent, and can be implemented as a computationally very efficient algorithm for application. It can be normalized, and tested for statistical significance. Different from the previous work along this line where only information flows are estimated, here an algorithm is also implemented to quantify the influence of a unit to itself. While this forms a challenge in some causal inferences, here it comes naturally, and hence the identification of self-loops in a causal graph is fulfilled automatically as the causalities along edges are inferred. To demonstrate the power of the approach, presented here are two applications in extreme situations. The first is a network of multivariate processes buried in heavy noises (with the noise-to-signal ratio exceeding 100), and the second a network with nearly synchronized chaotic oscillators. In both graphs, confounding processes exist. While it seems to be a huge challenge to reconstruct from given series these causal graphs, an easy application of the algorithm immediately reveals the desideratum. Particularly, the confounding processes have been accurately differentiated. Considering the surge of interest in the community, this study is very timely.