Self-Portrait of the Focusing Process in Speckle: III. Tailoring Complex Spatio-Temporal Focusing Laws To Overcome Reverberations in Reflection Imaging

This is the third article in a series of three dealing with the exploitation of speckle for imaging purposes. In complex media, a fundamental limit is the multiple scattering phenomenon that completely blurs the imaging process in depth. Matrix imaging can provide a relevant framework for solving this problem. As it proved to be an adequate tool for probing reverberations in speckle [E. Giraudat et al., Part I], we will show how it can be used to tailor complex spatio-temporal focusing laws to monitor the interference between the multiply-reflected paths and the ballistic component of the wave-field. To do so, we extend the distortion matrix concept to the frequency domain. An iterative phase reversal process operated from the space-time Fourier space is then used to compensate for reverberations and optimize both the axial and transverse resolution of the confocal image. Here, we first present an experimental proof-of-concept consisting in imaging a tissue-mimicking phantom through a reverberating plate before outlining the potential and the limits of this strategy for transcranial ultrasound and beyond.

Physics-Based Learning of the Wave Speed Landscape in Complex Media

Wave velocity is a key parameter for imaging complex media, but in vivo measurements are typically limited to reflection geometries, where only backscattered waves from short-scale heterogeneities are accessible. As a result, conventional reflection imaging fails to recover large-scale variations of the wave velocity landscape. Here we show that matrix imaging overcomes this limitation by exploiting the quality of wave focusing as an intrinsic guide star. We model wave propagation as a trainable multi-layer network that leverages optimization and deep learning tools to infer the wave velocity distribution. We validate this approach through ultrasound experiments on tissue-mimicking phantoms and human breast tissues, demonstrating its potential for tumour detection and characterization. Our method is broadly applicable to any kind of waves and media for which a reflection matrix can be measured.

Fingerprint Matrix Concept for Detecting, Localizing and Characterizing Targets in Complex Media

As waves propagate through a complex medium, they undergo multiple scattering events. This phenomenon is detrimental to imaging, as it causes a full blurring of the image beyond a transport mean free path. Here, we show how to detect, localize, and characterize any scattering target through the reflection matrix of the complex medium in which this target is embedded and thus hidden from direct view. More precisely, we introduce a fingerprint operator that contains the specific signature of the target with respect to its environment. Applied to the recorded reflection matrix, this operator provides a likelihood index of the target in any given state, despite the scattering fog induced by the surrounding environment. This state can be the target position for localization purposes, its shape for characterization, or any other parameter that influences the target response. Our concept is versatile and broadly applicable to different type of waves for which multi-element technology allows a reflection matrix to be measured. We demonstrate this here explicitly by performing different proof-of-concept experiments with ultrasound on targets buried inside a strongly scattering granular suspension, on lesion markers for clinical applications, and on the architecture of muscle tissue.

Reflection Matrix Imaging for Wave Velocity Tomography

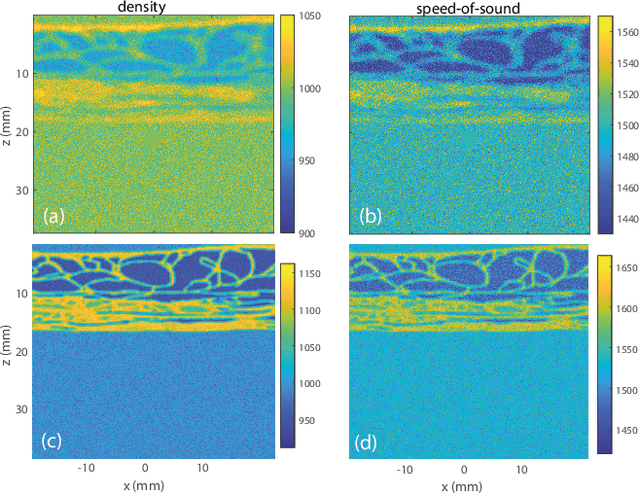
Besides controlling wave trajectory inside complex media, wave velocity constitutes a relevant bio-marker for medical imaging. In a transmission configuration, wave-front distortions can be unscrambled to provide a map of the wave velocity landscape $c(\mathbf{r})$. However, most in-vivo applications correspond to a reflection configuration for which only back-scattered echoes generated by short-scale fluctuations of $c(\mathbf{r})$ can be harvested. Under a single scattering assumption, this speckle wave-field cannot provide the long-scale variations of $c(\mathbf{r})$. In this paper, we go beyond the first Born approximation and show how a map of $c(\mathbf{r})$ can be retrieved in epi-detection. To that aim, a reflection matrix approach of wave imaging is adopted. While standard reflection imaging methods generally rely on confocal focusing operations, matrix imaging consists in decoupling the location of the incident and received focal spots. Following this principle, a self-portrait of the focusing process can be obtained around each point of the medium. The Gouy phase shift exhibited by each focal spot is leveraged to finely monitor the wave velocity distribution $c(\mathbf{r})$ inside the medium. Experiment in a tissue-mimicking phantom and numerical simulations are first presented to validate our method. Speed-of-sound tomography is then applied to ultrasound data collected on the liver of a difficult-to-image patient. Beyond paving the way towards quantitative ultrasound, our approach can also be extremely rewarding for standard imaging. Indeed, each echo can be assigned to the actual position of a scatterer. It allows an absolute measurement of distance, an observable often used for diagnosis but generally extremely sensitive to wave velocity fluctuations.

Three-Dimensional Ultrasound Matrix Imaging

Matrix imaging paves the way towards a next revolution in wave physics. Based on the response matrix recorded between a set of sensors, it enables an optimized compensation of aberration phenomena and multiple scattering events that usually drastically hinder the focusing process in heterogeneous media. Although it gave rise to spectacular results in optical microscopy or seismic imaging, the success of matrix imaging has been so far relatively limited with ultrasonic waves because wave control is generally only performed with a linear array of transducers. In this paper, we extend ultrasound matrix imaging to a 3D geometry. Switching from a 1D to a 2D probe enables a much sharper estimation of the transmission matrix that links each transducer and each medium voxel. Here, we first present an experimental proof of concept on a tissue-mimicking phantom through ex-vivo tissues and then, show the potential of 3D matrix imaging for transcranial applications.

Ultrasound Matrix Imaging. II. The distortion matrix for aberration correction over multiple isoplanatic patches

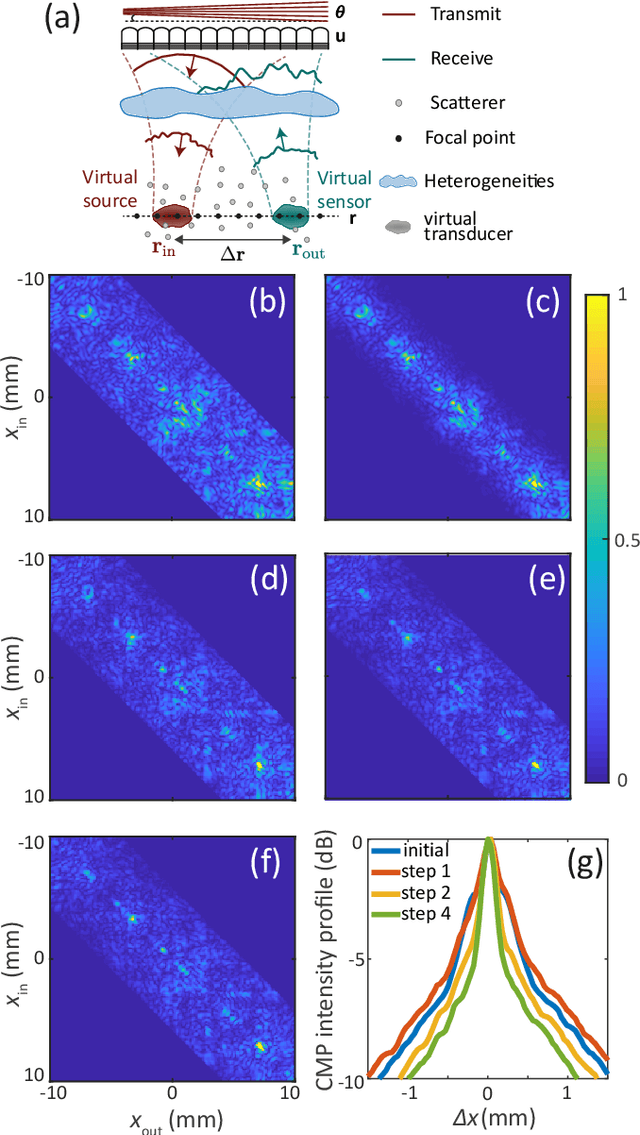
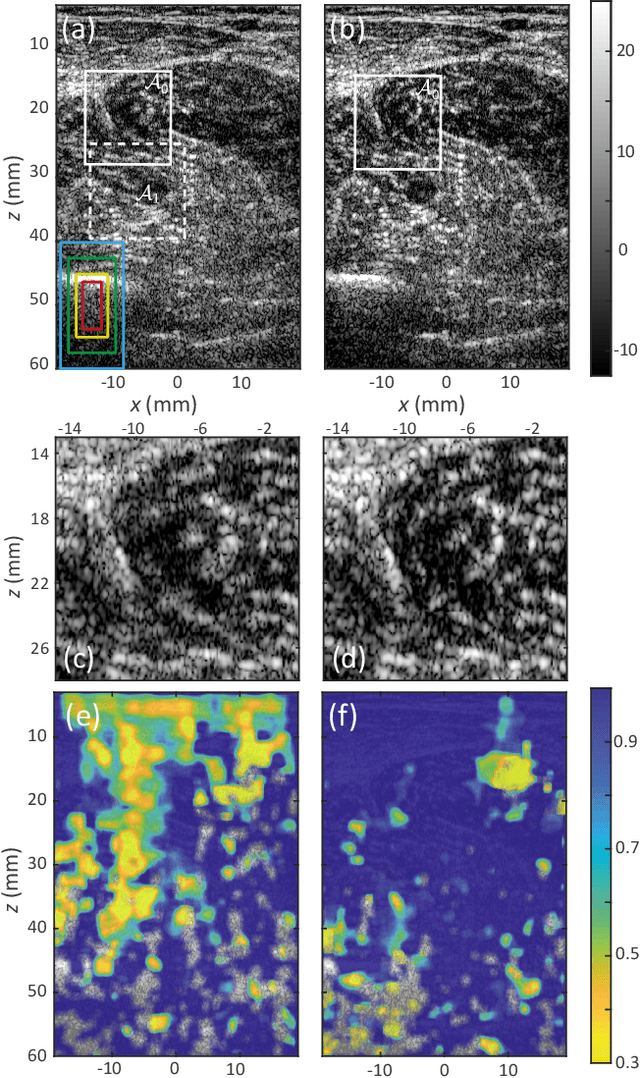
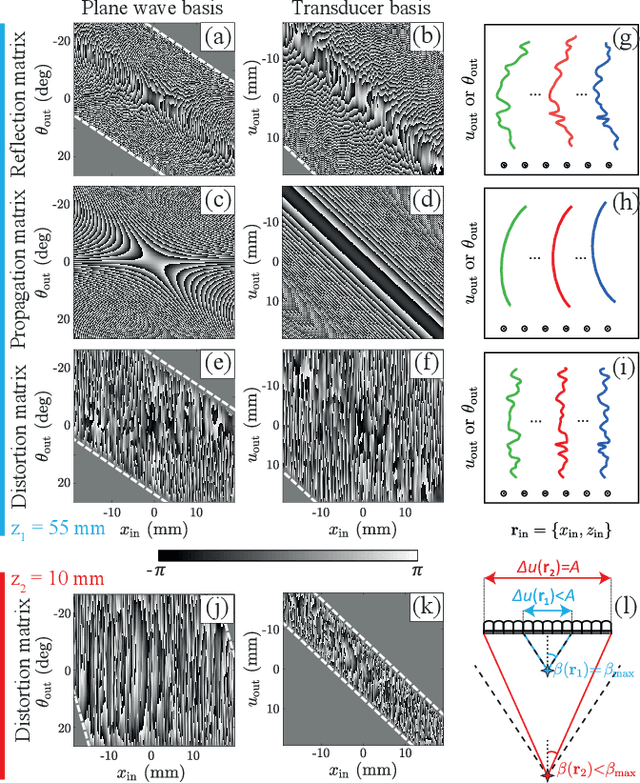
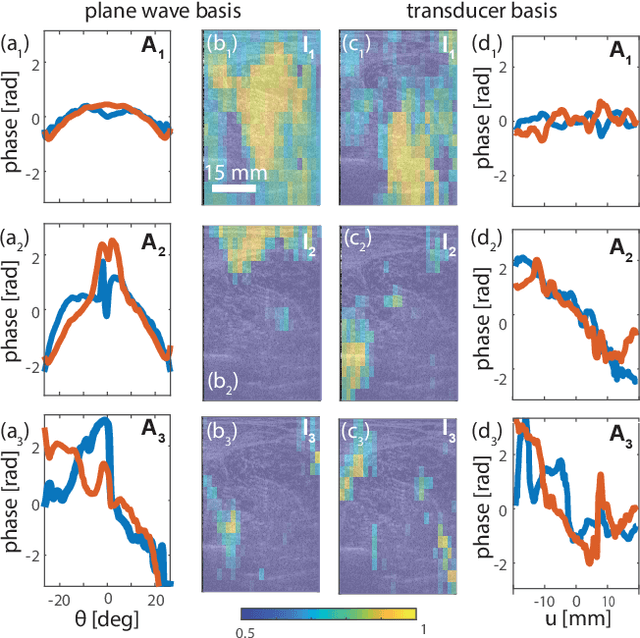
This is the second article in a series of two which report on a matrix approach for ultrasound imaging in heterogeneous media. This article describes the quantification and correction of aberration, i.e. the distortion of an image caused by spatial variations in the medium speed-of-sound. Adaptive focusing can compensate for aberration, but is only effective over a restricted area called the isoplanatic patch. Here, we use an experimentally-recorded matrix of reflected acoustic signals to synthesize a set of virtual transducers. We then examine wave propagation between these virtual transducers and an arbitrary correction plane. Such wave-fronts consist of two components: (i) An ideal geometric wave-front linked to diffraction and the input focusing point, and; (ii) Phase distortions induced by the speed-of-sound variations. These distortions are stored in a so-called distortion matrix, the singular value decomposition of which gives access to an optimized focusing law at any point. We show that, by decoupling the aberrations undergone by the outgoing and incoming waves and applying an iterative strategy, compensation for even high-order and spatially-distributed aberrations can be achieved. As a proof-of-concept, ultrasound matrix imaging (UMI) is applied to the in-vivo imaging of a human calf. A map of isoplanatic patches is retrieved and is shown to be strongly correlated with the arrangement of tissues constituting the medium. The corresponding focusing laws yield an ultrasound image with an optimal contrast and a transverse resolution close to the ideal value predicted by diffraction theory. UMI thus provides a flexible and powerful route towards computational ultrasound.

Ultrasound Matrix Imaging. I. The focused reflection matrix and the F-factor

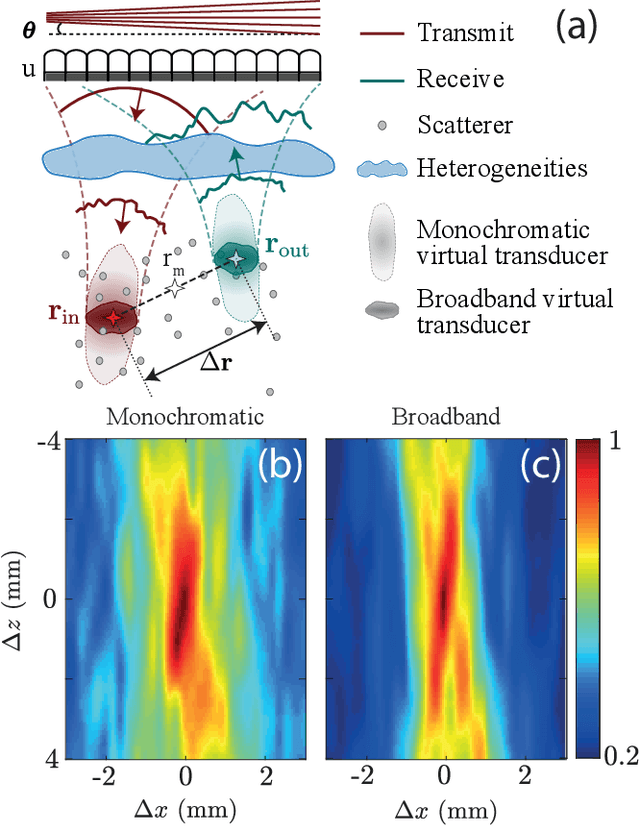
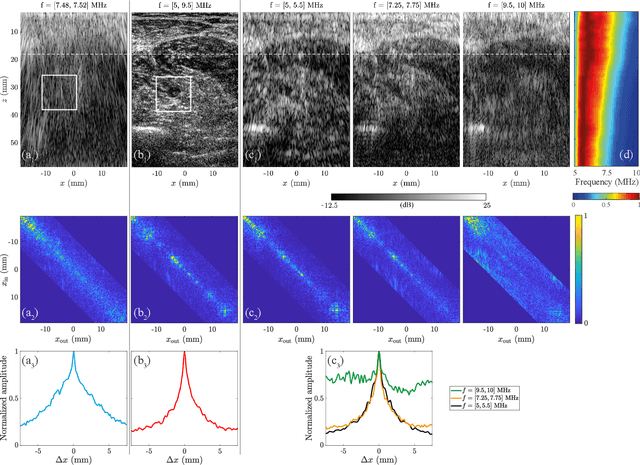
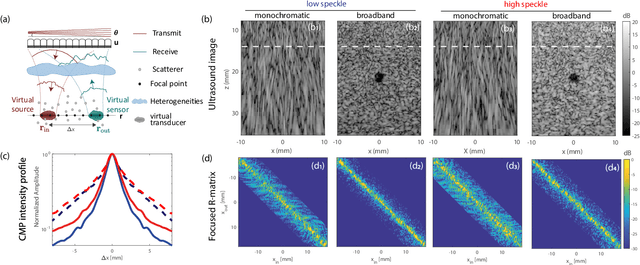
This is the first article in a series of two dealing with a matrix approach \alex{for} aberration quantification and correction in ultrasound imaging. Advanced synthetic beamforming relies on a double focusing operation at transmission and reception on each point of the medium. Ultrasound matrix imaging (UMI) consists in decoupling the location of these transmitted and received focal spots. The response between those virtual transducers form the so-called focused reflection matrix that actually contains much more information than a raw ultrasound image. In this paper, a time-frequency analysis of this matrix is performed, which highlights the single and multiple scattering contributions as well as the impact of aberrations in the monochromatic and broadband regimes. Interestingly, this analysis enables the measurement of the incoherent input-output point spread function at any pixel of this image. A focusing criterion can then be built, and its evolution used to quantify the amount of aberration throughout the ultrasound image. In contrast to the standard coherence factor used in the literature, this new indicator is robust to multiple scattering and electronic noise, thereby providing a highly contrasted map of the focusing quality. As a proof-of-concept, UMI is applied here to the in-vivo study of a human calf, but it can be extended to any kind of ultrasound diagnosis or non-destructive evaluation.