Ultrasound Matrix Imaging. II. The distortion matrix for aberration correction over multiple isoplanatic patches

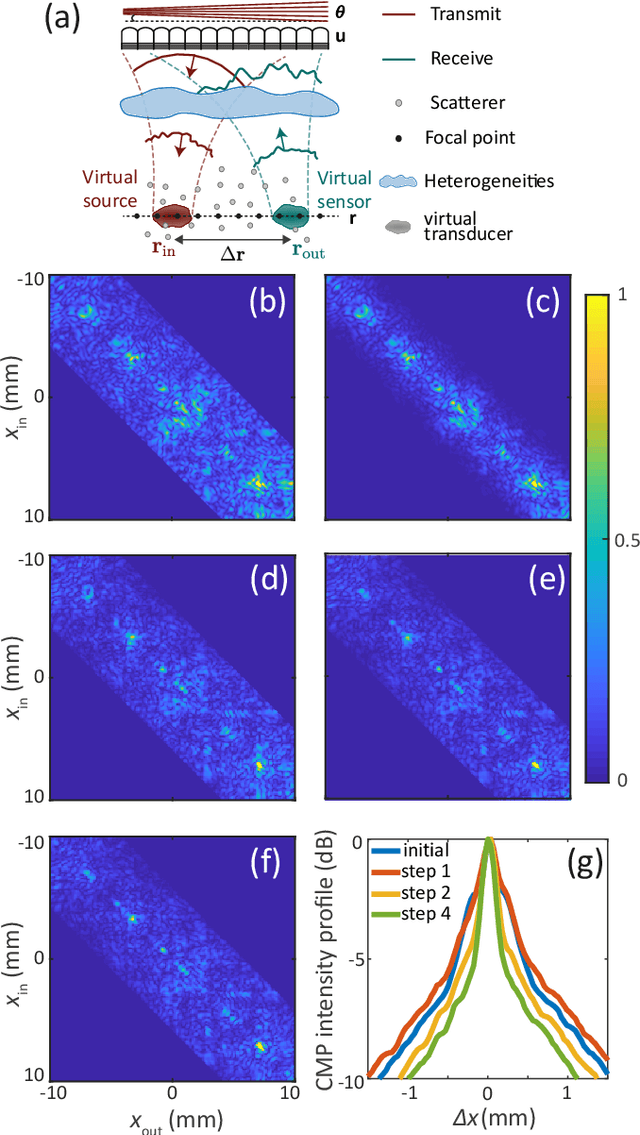
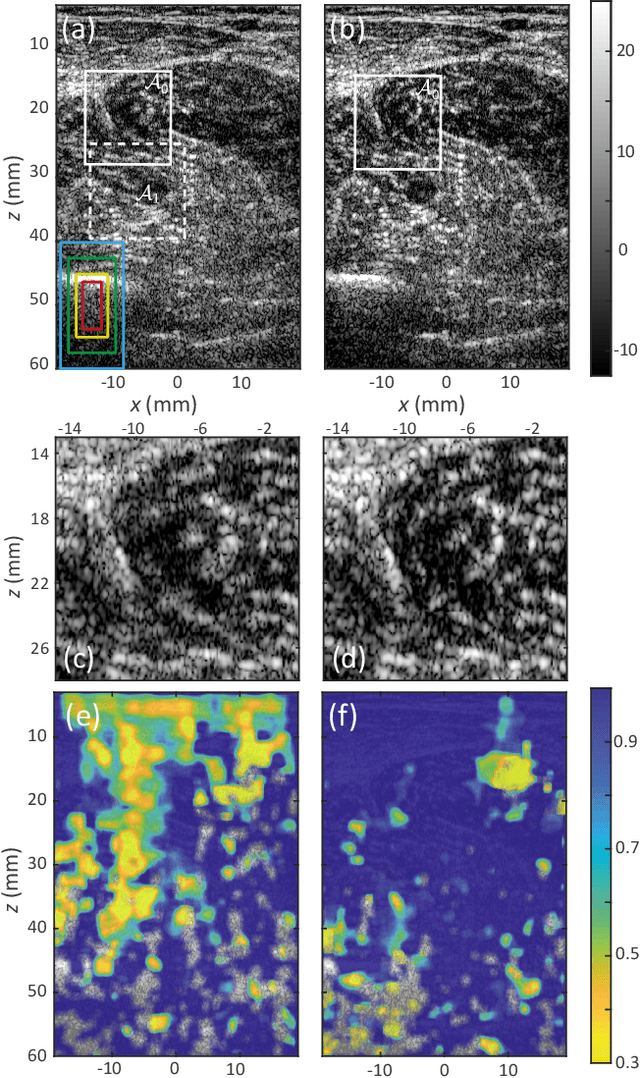
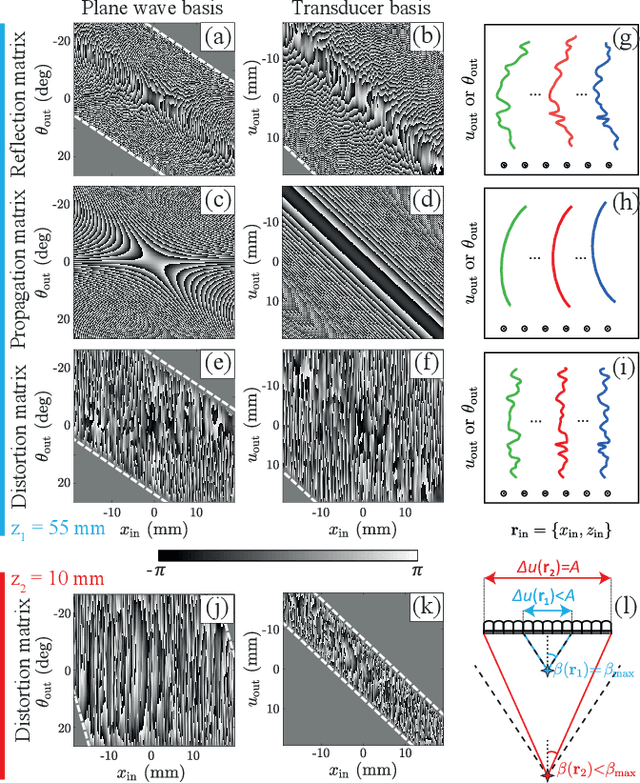
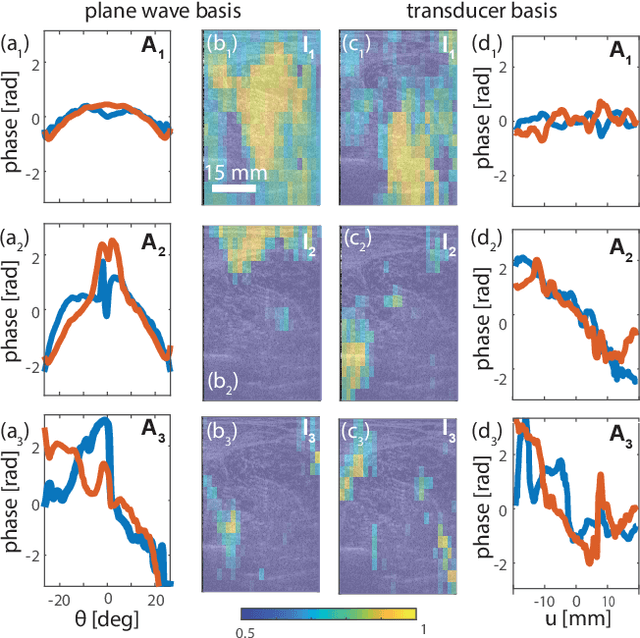
This is the second article in a series of two which report on a matrix approach for ultrasound imaging in heterogeneous media. This article describes the quantification and correction of aberration, i.e. the distortion of an image caused by spatial variations in the medium speed-of-sound. Adaptive focusing can compensate for aberration, but is only effective over a restricted area called the isoplanatic patch. Here, we use an experimentally-recorded matrix of reflected acoustic signals to synthesize a set of virtual transducers. We then examine wave propagation between these virtual transducers and an arbitrary correction plane. Such wave-fronts consist of two components: (i) An ideal geometric wave-front linked to diffraction and the input focusing point, and; (ii) Phase distortions induced by the speed-of-sound variations. These distortions are stored in a so-called distortion matrix, the singular value decomposition of which gives access to an optimized focusing law at any point. We show that, by decoupling the aberrations undergone by the outgoing and incoming waves and applying an iterative strategy, compensation for even high-order and spatially-distributed aberrations can be achieved. As a proof-of-concept, ultrasound matrix imaging (UMI) is applied to the in-vivo imaging of a human calf. A map of isoplanatic patches is retrieved and is shown to be strongly correlated with the arrangement of tissues constituting the medium. The corresponding focusing laws yield an ultrasound image with an optimal contrast and a transverse resolution close to the ideal value predicted by diffraction theory. UMI thus provides a flexible and powerful route towards computational ultrasound.