Convergence Guarantees for Neural Network-Based Hamilton-Jacobi Reachability

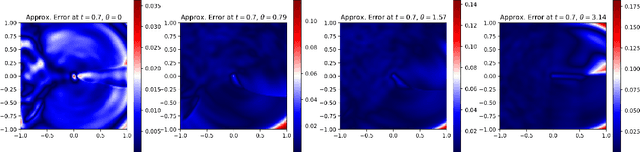
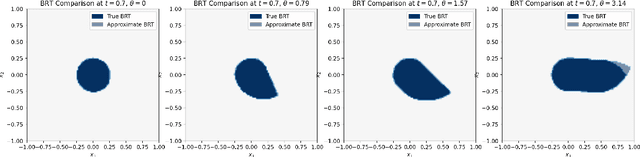
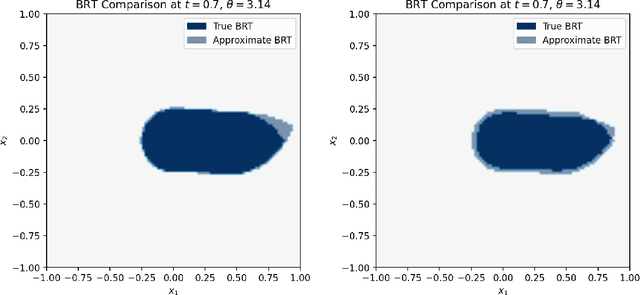
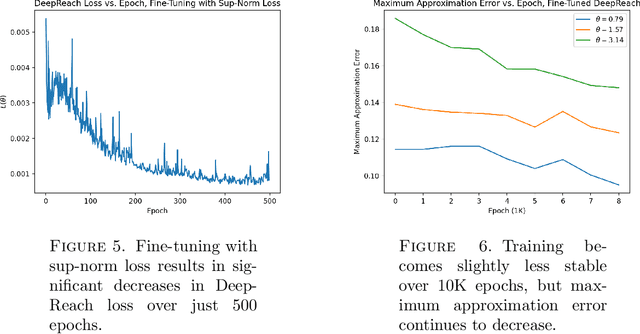
We provide a novel uniform convergence guarantee for DeepReach, a deep learning-based method for solving Hamilton-Jacobi-Isaacs (HJI) equations associated with reachability analysis. Specifically, we show that the DeepReach algorithm, as introduced by Bansal et al. in their eponymous paper from 2020, is stable in the sense that if the loss functional for the algorithm converges to zero, then the resulting neural network approximation converges uniformly to the classical solution of the HJI equation, assuming that a classical solution exists. We also provide numerical tests of the algorithm, replicating the experiments provided in the original DeepReach paper and empirically examining the impact that training with a supremum norm loss metric has on approximation error.

Convergence of the Deep Galerkin Method for Mean Field Control Problems

We establish the convergence of the deep Galerkin method (DGM), a deep learning-based scheme for solving high-dimensional nonlinear PDEs, for Hamilton-Jacobi-Bellman (HJB) equations that arise from the study of mean field control problems (MFCPs). Based on a recent characterization of the value function of the MFCP as the unique viscosity solution of an HJB equation on the simplex, we establish both an existence and convergence result for the DGM. First, we show that the loss functional of the DGM can be made arbitrarily small given that the value function of the MFCP possesses sufficient regularity. Then, we show that if the loss functional of the DGM converges to zero, the corresponding neural network approximators must converge uniformly to the true value function on the simplex. We also provide numerical experiments demonstrating the DGM's ability to generalize to high-dimensional HJB equations.