Convergence Guarantees for Neural Network-Based Hamilton-Jacobi Reachability
Paper and Code
Oct 03, 2024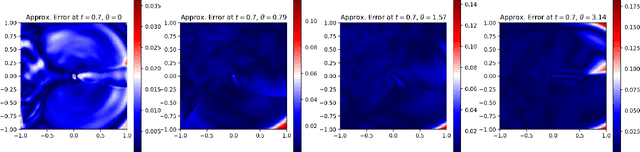
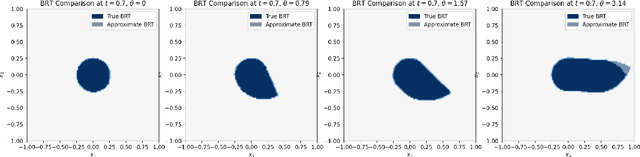
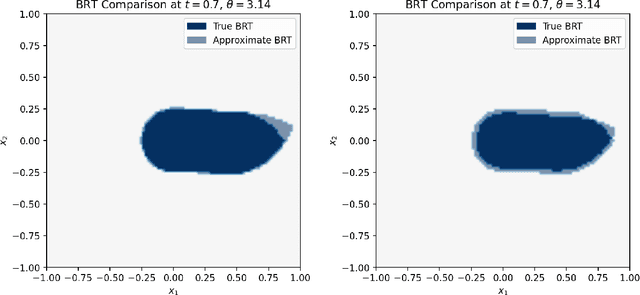
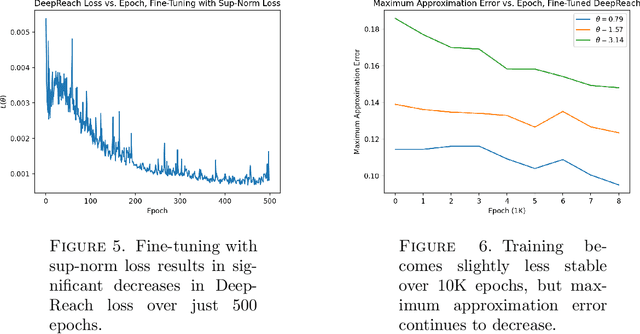
We provide a novel uniform convergence guarantee for DeepReach, a deep learning-based method for solving Hamilton-Jacobi-Isaacs (HJI) equations associated with reachability analysis. Specifically, we show that the DeepReach algorithm, as introduced by Bansal et al. in their eponymous paper from 2020, is stable in the sense that if the loss functional for the algorithm converges to zero, then the resulting neural network approximation converges uniformly to the classical solution of the HJI equation, assuming that a classical solution exists. We also provide numerical tests of the algorithm, replicating the experiments provided in the original DeepReach paper and empirically examining the impact that training with a supremum norm loss metric has on approximation error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge