Muon$^p$: Muon with Fractional Spectral Powers

Muon is an increasingly widely used optimizer that replaces a gradient $G=USV^\top$ with its polar factor $UV^\top$, thereby flattening the singular spectrum. However, full flattening discards singular-value information that may matter for adaptation. We introduce Muon$^p$, a Muon-style optimizer that instead uses fractional spectral-power updates $US^pV^\top$ for rational $p\in(0,1)$, interpolating between Muon and gradient descent. To make it practical, we prove that fractional spectral powers cannot be computed by any fixed univariate polynomial iteration, and furthermore derive low-degree odd bivariate recurrences that approximate $US^pV^\top$ using only matrix multiplications, preserving Muon's matrix-multiplication-only structure and compute complexity. We show that Muon$^p$ maximizes the linear improvement in loss under the Schatten $q$-norm for $q=1+\frac{1}{p}$. Empirically, Muon$^p$ is especially effective for finetuning: on billion-scale models, Muon$^p$ improves validation perplexity and downstream task performance. We further analyze when Muon$^p$ is less suitable, through the lens of spectral geometry. Our results reveal important insights on when preserving the singular spectrum can bring significant gains, and introduce a principled way to achieve them.

HNHN: Hypergraph Networks with Hyperedge Neurons

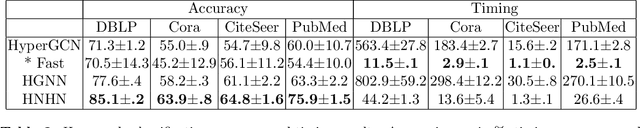
Hypergraphs provide a natural representation for many real world datasets. We propose a novel framework, HNHN, for hypergraph representation learning. HNHN is a hypergraph convolution network with nonlinear activation functions applied to both hypernodes and hyperedges, combined with a normalization scheme that can flexibly adjust the importance of high-cardinality hyperedges and high-degree vertices depending on the dataset. We demonstrate improved performance of HNHN in both classification accuracy and speed on real world datasets when compared to state of the art methods.

COPT: Coordinated Optimal Transport on Graphs

We introduce COPT, a novel distance metric between graphs defined via an optimization routine, computing a coordinated pair of optimal transport maps simultaneously. This is an unsupervised way to learn general-purpose graph representations, it can be used for both graph sketching and graph comparison. COPT involves simultaneously optimizing dual transport plans, one between the vertices of two graphs, and another between graph signal probability distributions. We show both theoretically and empirically that our method preserves important global structural information on graphs, in particular spectral information, making it well-suited for tasks on graphs including retrieval, classification, summarization, and visualization.