The LG Fibration

Deep Learning has significantly impacted the application of data-to-decision throughout research and industry, however, they lack a rigorous mathematical foundation, which creates situations where algorithmic results fail to be practically invertible. In this paper we present a nearly invertible mapping between $\mathbb{R}^{2^n}$ and $\mathbb{R}^{n+1}$ via a topological connection between $S^{2^n-1}$ and $S^n$. Throughout the paper we utilize the algebra of Multicomplex rotation groups and polyspherical coordinates to define two maps: the first is a contraction from $S^{2^n-1}$ to $\displaystyle \otimes^n_{k=1} SO(2)$, and the second is a projection from $\displaystyle \otimes^n_{k=1} SO(2)$ to $S^{n}$. Together these form a composite map that we call the LG Fibration. In analogy to the generation of Hopf Fibration using Hypercomplex geometry from $S^{(2n-1)} \mapsto CP^n$, our fibration uses Multicomplex geometry to project $S^{2^n-1}$ onto $S^n$. We also investigate the algebraic properties of the LG Fibration, ultimately deriving a distance difference function to determine which pairs of vectors have an invariant inner product under the transformation. The LG Fibration has applications to Machine Learning and AI, in analogy to the current applications of Hopf Fibrations in adaptive UAV control. Furthermore, the ability to invert the LG Fibration for nearly all elements allows for the development of Machine Learning algorithms that may avoid the issues of uncertainty and reproducibility that currently plague contemporary methods. The primary result of this paper is a novel method of nearly invertible geometric dimensional reduction from $S^{2^n-1}$ to $S^n$, which has the capability to extend the research in both mathematics and AI, including but not limited to the fields of homotopy groups of spheres, algebraic topology, machine learning, and algebraic biology.

EEG Machine Learning for Analysis of Mild Traumatic Brain Injury: A survey

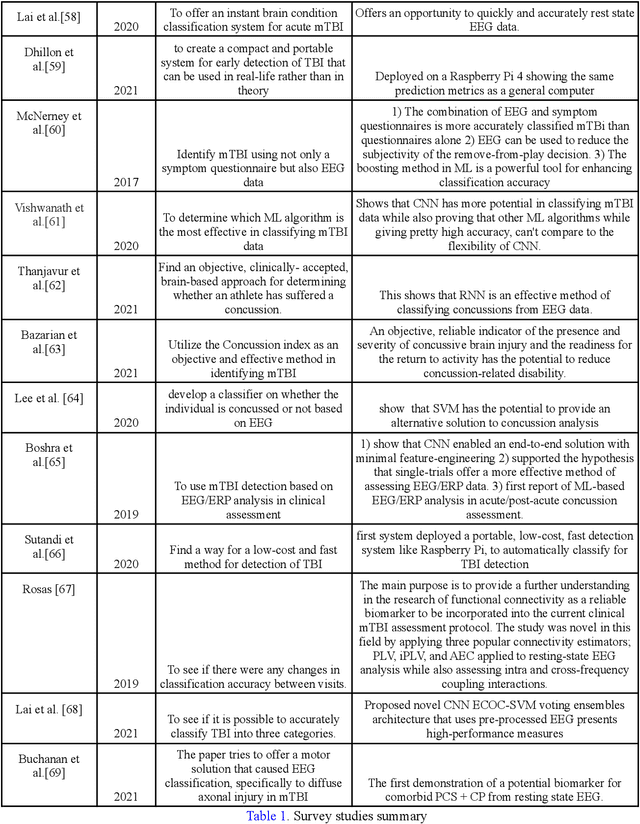
Mild Traumatic Brain Injury (mTBI) is a common brain injury and affects a diverse group of people: soldiers, constructors, athletes, drivers, children, elders, and nearly everyone. Thus, having a well-established, fast, cheap, and accurate classification method is crucial for the well-being of people around the globe. Luckily, using Machine Learning (ML) on electroencephalography (EEG) data shows promising results. This survey analyzed the most cutting-edge articles from 2017 to the present. The articles were searched from the Google Scholar database and went through an elimination process based on our criteria. We reviewed, summarized, and compared the fourteen most cutting-edge machine learning research papers for predicting and classifying mTBI in terms of 1) EEG data types, 2) data preprocessing methods, 3) machine learning feature representations, 4) feature extraction methods, and 5) machine learning classifiers and predictions. The most common EEG data type was human resting-state EEG, with most studies using filters to clean the data. The power spectral, especially alpha and theta power, was the most prevalent feature. The other non-power spectral features, such as entropy, also show their great potential. The Fourier transform is the most common feature extraction method while using neural networks as automatic feature extraction generally returns a high accuracy result. Lastly, Support Vector Machine (SVM) was our survey's most common ML classifier due to its lower computational complexity and solid mathematical theoretical basis. The purpose of this study was to collect and explore a sparsely populated sector of ML, and we hope that our survey has shined some light on the inherent trends, advantages, disadvantages, and preferences of the current state of machine learning-based EEG analysis for mTBI.

Machine Learning-based EEG Applications and Markets

This paper addresses both the various EEG applications and the current EEG market ecosystem propelled by machine learning. Increasingly available open medical and health datasets using EEG encourage data-driven research with a promise of improving neurology for patient care through knowledge discovery and machine learning data science algorithm development. This effort leads to various kinds of EEG developments and currently forms a new EEG market. This paper attempts to do a comprehensive survey on the EEG market and covers the six significant applications of EEG, including diagnosis/screening, drug development, neuromarketing, daily health, metaverse, and age/disability assistance. The highlight of this survey is on the compare and contrast between the research field and the business market. Our survey points out the current limitations of EEG and indicates the future direction of research and business opportunity for every EEG application listed above. Based on our survey, more research on machine learning-based EEG applications will lead to a more robust EEG-related market. More companies will use the research technology and apply it to real-life settings. As the EEG-related market grows, the EEG-related devices will collect more EEG data, and there will be more EEG data available for researchers to use in their study, coming back as a virtuous cycle. Our market analysis indicates that research related to the use of EEG data and machine learning in the six applications listed above points toward a clear trend in the growth and development of the EEG ecosystem and machine learning world.

Accelerometer-Based Gait Segmentation: Simultaneously User and Adversary Identification

In this paper, we introduce a new gait segmentation method based on accelerometer data and develop a new distance function between two time series, showing novel and effectiveness in simultaneously identifying user and adversary. Comparing with the normally used Neural Network methods, our approaches use geometric features to extract walking cycles more precisely and employ a new similarity metric to conduct user-adversary identification. This new technology for simultaneously identify user and adversary contributes to cybersecurity beyond user-only identification. In particular, the new technology is being applied to cell phone recorded walking data and performs an accuracy of $98.79\%$ for 6 classes classification (user-adversary identification) and $99.06\%$ for binary classification (user only identification). In addition to walking signal, our approach works on walking up, walking down and mixed walking signals. This technology is feasible for both large and small data set, overcoming the current challenges facing to Neural Networks such as tuning large number of hyper-parameters for large data sets and lacking of training data for small data sets. In addition, the new distance function developed here can be applied in any signal analysis.

A Randomized Algorithm for Preconditioner Selection

The task of choosing a preconditioner $\boldsymbol{M}$ to use when solving a linear system $\boldsymbol{Ax}=\boldsymbol{b}$ with iterative methods is difficult. For instance, even if one has access to a collection $\boldsymbol{M}_1,\boldsymbol{M}_2,\ldots,\boldsymbol{M}_n$ of candidate preconditioners, it is currently unclear how to practically choose the $\boldsymbol{M}_i$ which minimizes the number of iterations of an iterative algorithm to achieve a suitable approximation to $\boldsymbol{x}$. This paper makes progress on this sub-problem by showing that the preconditioner stability $\|\boldsymbol{I}-\boldsymbol{M}^{-1}\boldsymbol{A}\|_\mathsf{F}$, known to forecast preconditioner quality, can be computed in the time it takes to run a constant number of iterations of conjugate gradients through use of sketching methods. This is in spite of folklore which suggests the quantity is impractical to compute, and a proof we give that ensures the quantity could not possibly be approximated in a useful amount of time by a deterministic algorithm. Using our estimator, we provide a method which can provably select the minimal stability preconditioner among $n$ candidates using floating point operations commensurate with running on the order of $n\log n$ steps of the conjugate gradients algorithm. Our method can also advise the practitioner to use no preconditioner at all if none of the candidates appears useful. The algorithm is extremely easy to implement and trivially parallelizable. In one of our experiments, we use our preconditioner selection algorithm to create to the best of our knowledge the first preconditioned method for kernel regression reported to never use more iterations than the non-preconditioned analog in standard tests.