Weici Pan
Online Optimization with Feedback Delay and Nonlinear Switching Cost
Oct 29, 2021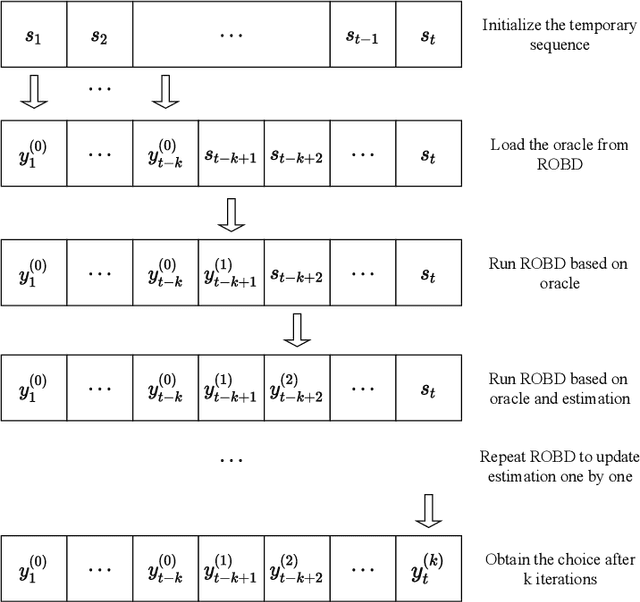
Abstract:We study a variant of online optimization in which the learner receives $k$-round $\textit{delayed feedback}$ about hitting cost and there is a multi-step nonlinear switching cost, i.e., costs depend on multiple previous actions in a nonlinear manner. Our main result shows that a novel Iterative Regularized Online Balanced Descent (iROBD) algorithm has a constant, dimension-free competitive ratio that is $O(L^{2k})$, where $L$ is the Lipschitz constant of the switching cost. Additionally, we provide lower bounds that illustrate the Lipschitz condition is required and the dependencies on $k$ and $L$ are tight. Finally, via reductions, we show that this setting is closely related to online control problems with delay, nonlinear dynamics, and adversarial disturbances, where iROBD directly offers constant-competitive online policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge