Diffusion-based Semi-supervised Spectral Algorithm for Regression on Manifolds

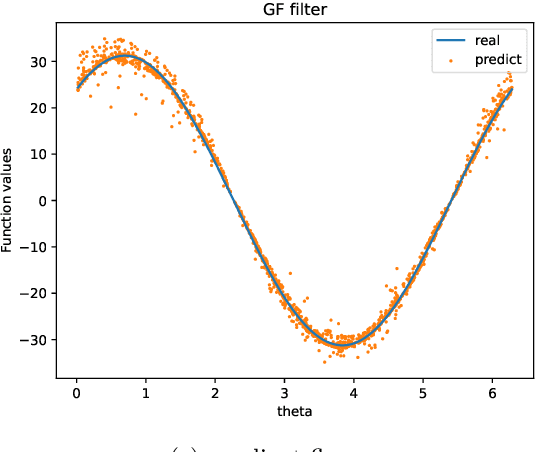
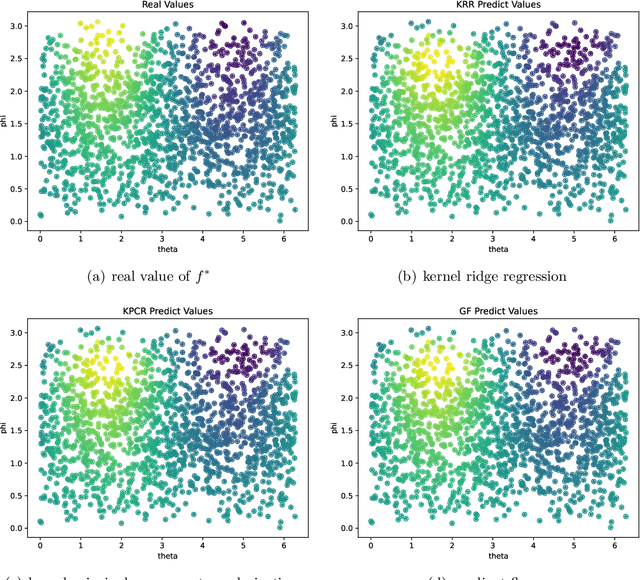
We introduce a novel diffusion-based spectral algorithm to tackle regression analysis on high-dimensional data, particularly data embedded within lower-dimensional manifolds. Traditional spectral algorithms often fall short in such contexts, primarily due to the reliance on predetermined kernel functions, which inadequately address the complex structures inherent in manifold-based data. By employing graph Laplacian approximation, our method uses the local estimation property of heat kernel, offering an adaptive, data-driven approach to overcome this obstacle. Another distinct advantage of our algorithm lies in its semi-supervised learning framework, enabling it to fully use the additional unlabeled data. This ability enhances the performance by allowing the algorithm to dig the spectrum and curvature of the data manifold, providing a more comprehensive understanding of the dataset. Moreover, our algorithm performs in an entirely data-driven manner, operating directly within the intrinsic manifold structure of the data, without requiring any predefined manifold information. We provide a convergence analysis of our algorithm. Our findings reveal that the algorithm achieves a convergence rate that depends solely on the intrinsic dimension of the underlying manifold, thereby avoiding the curse of dimensionality associated with the higher ambient dimension.

Spectral Algorithms on Manifolds through Diffusion

The existing research on spectral algorithms, applied within a Reproducing Kernel Hilbert Space (RKHS), has primarily focused on general kernel functions, often neglecting the inherent structure of the input feature space. Our paper introduces a new perspective, asserting that input data are situated within a low-dimensional manifold embedded in a higher-dimensional Euclidean space. We study the convergence performance of spectral algorithms in the RKHSs, specifically those generated by the heat kernels, known as diffusion spaces. Incorporating the manifold structure of the input, we employ integral operator techniques to derive tight convergence upper bounds concerning generalized norms, which indicates that the estimators converge to the target function in strong sense, entailing the simultaneous convergence of the function itself and its derivatives. These bounds offer two significant advantages: firstly, they are exclusively contingent on the intrinsic dimension of the input manifolds, thereby providing a more focused analysis. Secondly, they enable the efficient derivation of convergence rates for derivatives of any k-th order, all of which can be accomplished within the ambit of the same spectral algorithms. Furthermore, we establish minimax lower bounds to demonstrate the asymptotic optimality of these conclusions in specific contexts. Our study confirms that the spectral algorithms are practically significant in the broader context of high-dimensional approximation.