Deep Statistical Solver for Distribution System State Estimation

Implementing accurate Distribution System State Estimation (DSSE) faces several challenges, among which the lack of observability and the high density of the distribution system. While data-driven alternatives based on Machine Learning models could be a choice, they suffer in DSSE because of the lack of labeled data. In fact, measurements in the distribution system are often noisy, corrupted, and unavailable. To address these issues, we propose the Deep Statistical Solver for Distribution System State Estimation (DSS$^2$), a deep learning model based on graph neural networks (GNNs) that accounts for the network structure of the distribution system and for the physical governing power flow equations. DSS$^2$ leverages hypergraphs to represent the heterogeneous components of the distribution systems and updates their latent representations via a node-centric message-passing scheme. A weakly supervised learning approach is put forth to train the DSS$^2$ in a learning-to-optimize fashion w.r.t. the Weighted Least Squares loss with noisy measurements and pseudomeasurements. By enforcing the GNN output into the power flow equations and the latter into the loss function, we force the DSS$^2$ to respect the physics of the distribution system. This strategy enables learning from noisy measurements, acting as an implicit denoiser, and alleviating the need for ideal labeled data. Extensive experiments with case studies on the IEEE 14-bus, 70-bus, and 179-bus networks showed the DSS$^2$ outperforms by a margin the conventional Weighted Least Squares algorithm in accuracy, convergence, and computational time, while being more robust to noisy, erroneous, and missing measurements. The DSS$^2$ achieves a competing, yet lower, performance compared with the supervised models that rely on the unrealistic assumption of having all the true labels.

GP-HD: Using Genetic Programming to Generate Dynamical Systems Models for Health Care

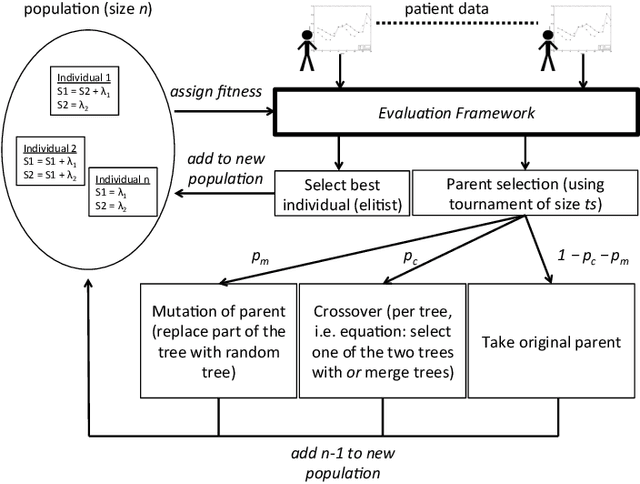
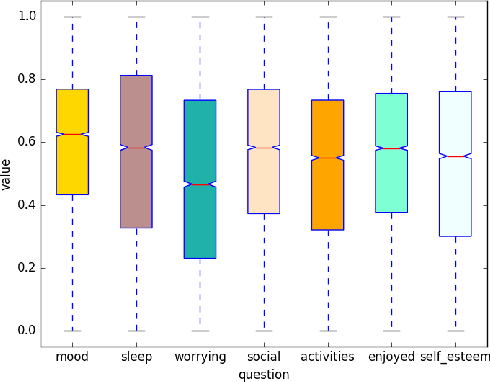
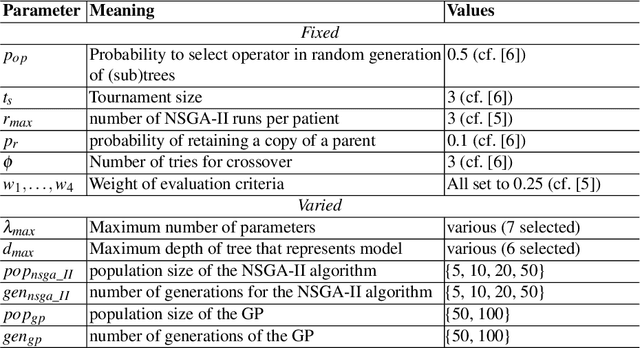
The huge wealth of data in the health domain can be exploited to create models that predict development of health states over time. Temporal learning algorithms are well suited to learn relationships between health states and make predictions about their future developments. However, these algorithms: (1) either focus on learning one generic model for all patients, providing general insights but often with limited predictive performance, or (2) learn individualized models from which it is hard to derive generic concepts. In this paper, we present a middle ground, namely parameterized dynamical systems models that are generated from data using a Genetic Programming (GP) framework. A fitness function suitable for the health domain is exploited. An evaluation of the approach in the mental health domain shows that performance of the model generated by the GP is on par with a dynamical systems model developed based on domain knowledge, significantly outperforms a generic Long Term Short Term Memory (LSTM) model and in some cases also outperforms an individualized LSTM model.