Stochastic Subgradient Descent Escapes Active Strict Saddles

In non-smooth stochastic optimization, we establish the non-convergence of the stochastic subgradient descent (SGD) to the critical points recently called active strict saddles by Davis and Drusvyatskiy. Such points lie on a manifold $M$ where the function $f$ has a direction of second-order negative curvature. Off this manifold, the norm of the Clarke subdifferential of $f$ is lower-bounded. We require two conditions on $f$. The first assumption is a Verdier stratification condition, which is a refinement of the popular Whitney stratification. It allows us to establish a reinforced version of the projection formula of Bolte \emph{et.al.} for Whitney stratifiable functions, and which is of independent interest. The second assumption, termed the angle condition, allows to control the distance of the iterates to $M$. When $f$ is weakly convex, our assumptions are generic. Consequently, generically in the class of definable weakly convex functions, the SGD converges to a local minimizer.

A Fully Stochastic Primal-Dual Algorithm

A new stochastic primal-dual algorithm for solving a composite optimization problem is proposed. It is assumed that all the functions/matrix used to define the optimization problem are given as statistical expectations. These expectations are unknown but revealed across time through i.i.d realizations. This covers the case of convex optimization under stochastic linear constraints. The proposed algorithm is proven to converge to a saddle point of the Lagrangian function. In the framework of the monotone operator theory, the convergence proof relies on recent results on the stochastic Forward Backward algorithm involving random monotone operators.

A Constant Step Stochastic Douglas-Rachford Algorithm with Application to Non Separable Regularizations

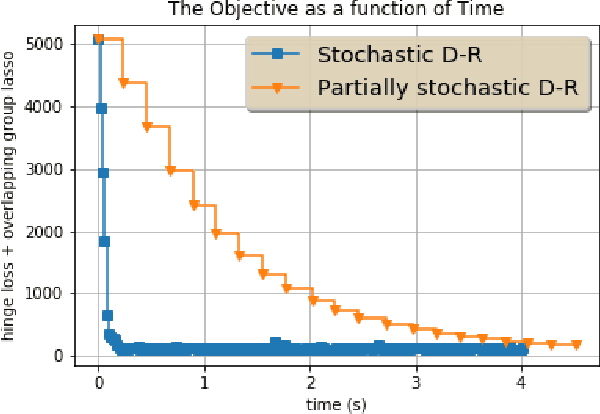
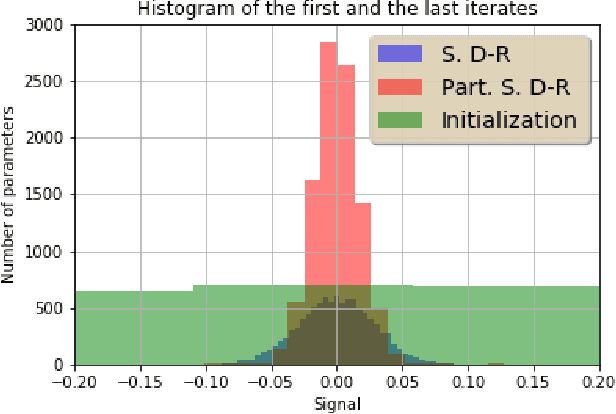
The Douglas Rachford algorithm is an algorithm that converges to a minimizer of a sum of two convex functions. The algorithm consists in fixed point iterations involving computations of the proximity operators of the two functions separately. The paper investigates a stochastic version of the algorithm where both functions are random and the step size is constant. We establish that the iterates of the algorithm stay close to the set of solution with high probability when the step size is small enough. Application to structured regularization is considered.

Snake: a Stochastic Proximal Gradient Algorithm for Regularized Problems over Large Graphs

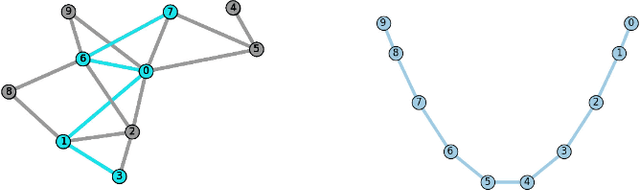
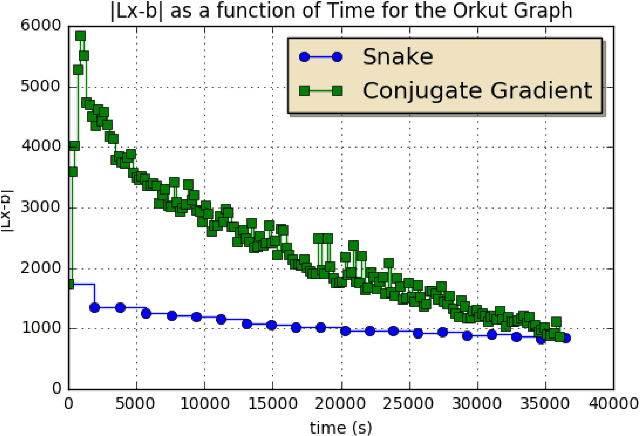
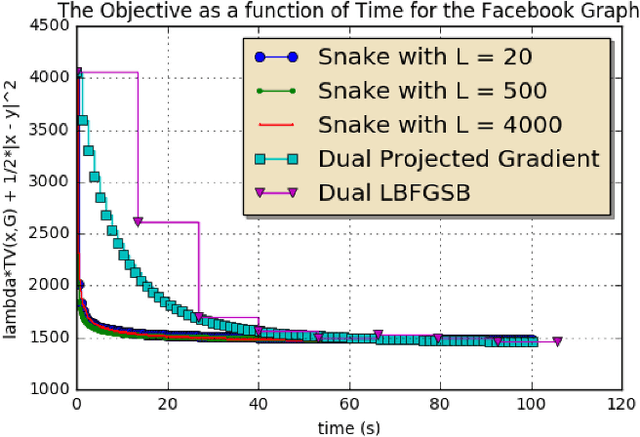
A regularized optimization problem over a large unstructured graph is studied, where the regularization term is tied to the graph geometry. Typical regularization examples include the total variation and the Laplacian regularizations over the graph. When applying the proximal gradient algorithm to solve this problem, there exist quite affordable methods to implement the proximity operator (backward step) in the special case where the graph is a simple path without loops. In this paper, an algorithm, referred to as "Snake", is proposed to solve such regularized problems over general graphs, by taking benefit of these fast methods. The algorithm consists in properly selecting random simple paths in the graph and performing the proximal gradient algorithm over these simple paths. This algorithm is an instance of a new general stochastic proximal gradient algorithm, whose convergence is proven. Applications to trend filtering and graph inpainting are provided among others. Numerical experiments are conducted over large graphs.