A Constant Step Stochastic Douglas-Rachford Algorithm with Application to Non Separable Regularizations
Paper and Code
Apr 03, 2018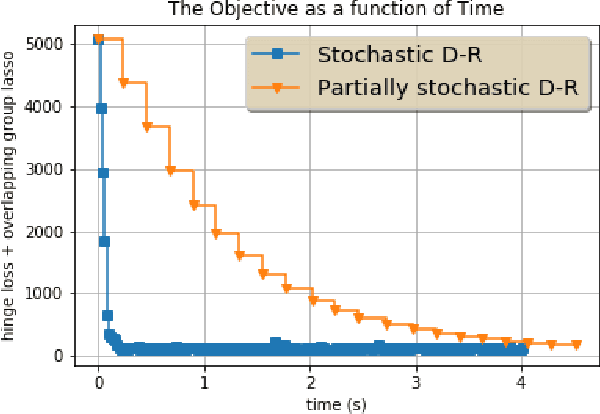
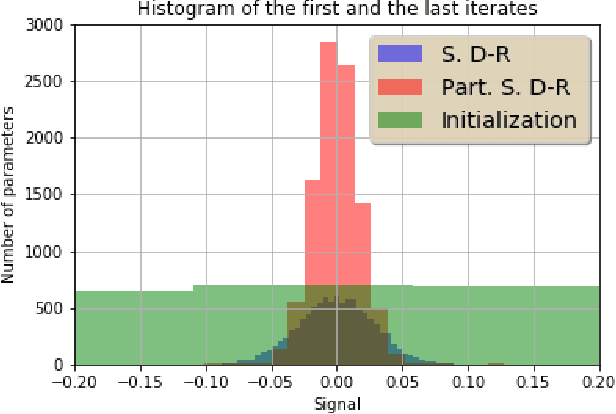
The Douglas Rachford algorithm is an algorithm that converges to a minimizer of a sum of two convex functions. The algorithm consists in fixed point iterations involving computations of the proximity operators of the two functions separately. The paper investigates a stochastic version of the algorithm where both functions are random and the step size is constant. We establish that the iterates of the algorithm stay close to the set of solution with high probability when the step size is small enough. Application to structured regularization is considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge