Snake: a Stochastic Proximal Gradient Algorithm for Regularized Problems over Large Graphs
Paper and Code
Dec 19, 2017
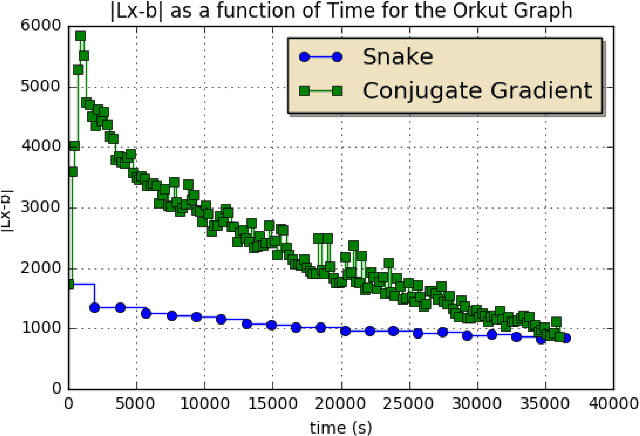
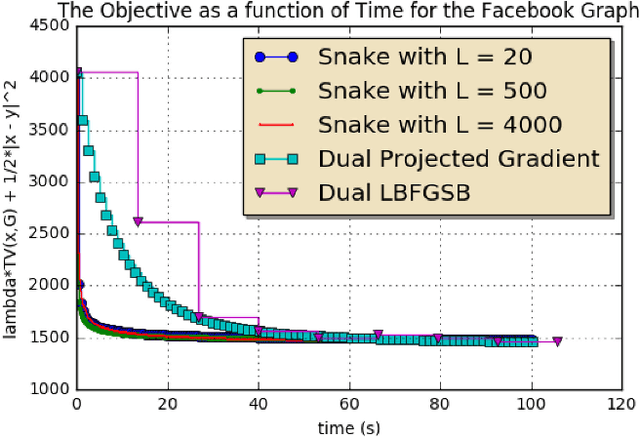
A regularized optimization problem over a large unstructured graph is studied, where the regularization term is tied to the graph geometry. Typical regularization examples include the total variation and the Laplacian regularizations over the graph. When applying the proximal gradient algorithm to solve this problem, there exist quite affordable methods to implement the proximity operator (backward step) in the special case where the graph is a simple path without loops. In this paper, an algorithm, referred to as "Snake", is proposed to solve such regularized problems over general graphs, by taking benefit of these fast methods. The algorithm consists in properly selecting random simple paths in the graph and performing the proximal gradient algorithm over these simple paths. This algorithm is an instance of a new general stochastic proximal gradient algorithm, whose convergence is proven. Applications to trend filtering and graph inpainting are provided among others. Numerical experiments are conducted over large graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge