Composition and decomposition of GANs

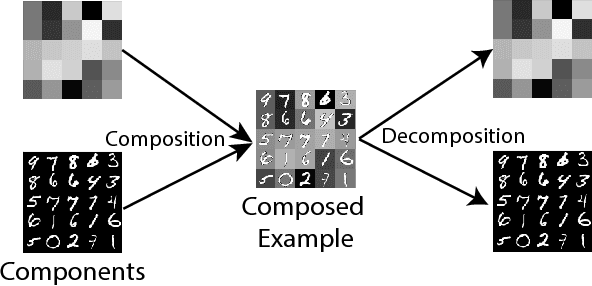
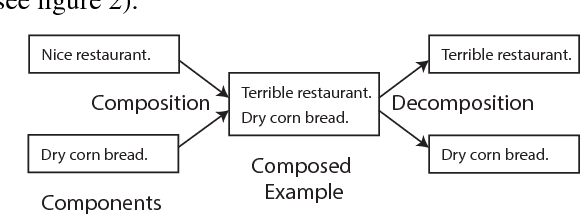
In this work, we propose a composition/decomposition framework for adversarially training generative models on composed data - data where each sample can be thought of as being constructed from a fixed number of components. In our framework, samples are generated by sampling components from component generators and feeding these components to a composition function which combines them into a "composed sample". This compositional training approach improves the modularity, extensibility and interpretability of Generative Adversarial Networks (GANs) - providing a principled way to incrementally construct complex models out of simpler component models, and allowing for explicit "division of responsibility" between these components. Using this framework, we define a family of learning tasks and evaluate their feasibility on two datasets in two different data modalities (image and text). Lastly, we derive sufficient conditions such that these compositional generative models are identifiable. Our work provides a principled approach to building on pre-trained generative models or for exploiting the compositional nature of data distributions to train extensible and interpretable models.

Degrees of Freedom in Deep Neural Networks

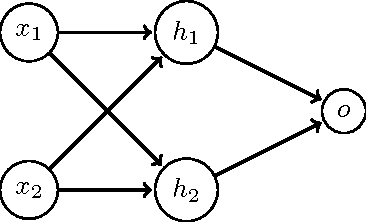
In this paper, we explore degrees of freedom in deep sigmoidal neural networks. We show that the degrees of freedom in these models is related to the expected optimism, which is the expected difference between test error and training error. We provide an efficient Monte-Carlo method to estimate the degrees of freedom for multi-class classification methods. We show degrees of freedom are lower than the parameter count in a simple XOR network. We extend these results to neural nets trained on synthetic and real data, and investigate impact of network's architecture and different regularization choices. The degrees of freedom in deep networks are dramatically smaller than the number of parameters, in some real datasets several orders of magnitude. Further, we observe that for fixed number of parameters, deeper networks have less degrees of freedom exhibiting a regularization-by-depth.