Global Convergence and Stability of Stochastic Gradient Descent

In machine learning, stochastic gradient descent (SGD) is widely deployed to train models using highly non-convex objectives with equally complex noise models. Unfortunately, SGD theory often makes restrictive assumptions that fail to capture the non-convexity of real problems, and almost entirely ignore the complex noise models that exist in practice. In this work, we make substantial progress on this shortcoming. First, we establish that SGD's iterates will either globally converge to a stationary point or diverge under nearly arbitrary nonconvexity and noise models. Under a slightly more restrictive assumption on the joint behavior of the non-convexity and noise model that generalizes current assumptions in the literature, we show that the objective function cannot diverge, even if the iterates diverge. As a consequence of our results, SGD can be applied to a greater range of stochastic optimization problems with confidence about its global convergence behavior and stability.

Stochastic Approximation for High-frequency Observations in Data Assimilation

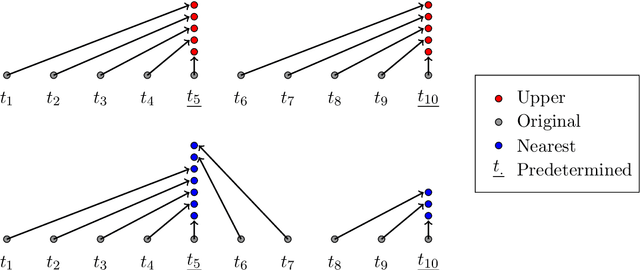
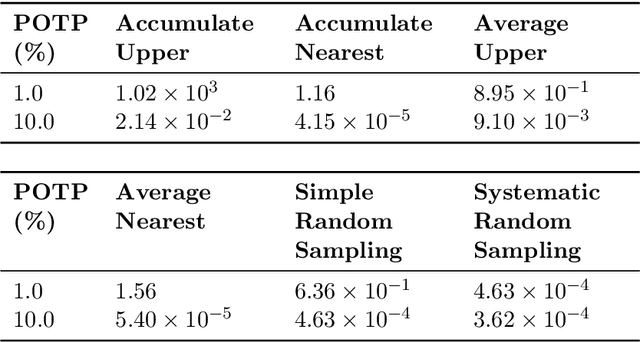
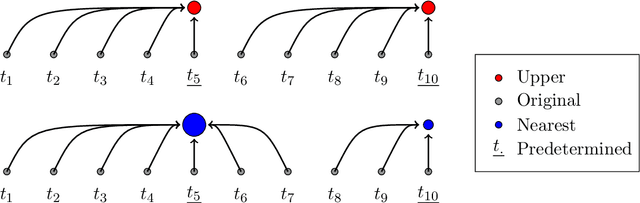
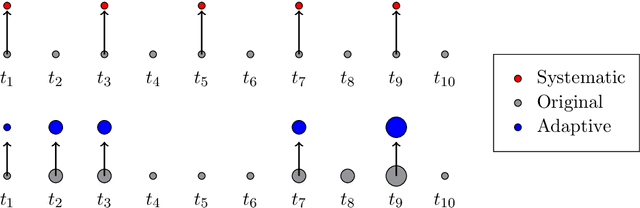
With the increasing penetration of high-frequency sensors across a number of biological and physical systems, the abundance of the resulting observations offers opportunities for higher statistical accuracy of down-stream estimates, but their frequency results in a plethora of computational problems in data assimilation tasks. The high-frequency of these observations has been traditionally dealt with by using data modification strategies such as accumulation, averaging, and sampling. However, these data modification strategies will reduce the quality of the estimates, which may be untenable for many systems. Therefore, to ensure high-quality estimates, we adapt stochastic approximation methods to address the unique challenges of high-frequency observations in data assimilation. As a result, we are able to produce estimates that leverage all of the observations in a manner that avoids the aforementioned computational problems and preserves the statistical accuracy of the estimates.

Stopping Criteria for, and Strong Convergence of, Stochastic Gradient Descent on Bottou-Curtis-Nocedal Functions

While Stochastic Gradient Descent (SGD) is a rather efficient algorithm for data-driven problems, it is an incomplete optimization algorithm as it lacks stopping criteria, which has limited its adoption in situations where such criteria are necessary. Unlike stopping criteria for deterministic methods, stopping criteria for SGD require a detailed understanding of (A) strong convergence, (B) whether the criteria will be triggered, (C) how false negatives are controlled, and (D) how false positives are controlled. In order to address these issues, we first prove strong global convergence (i.e., convergence with probability one) of SGD on a popular and general class of convex and nonconvex functions that are specified by, what we call, the Bottou-Curtis-Nocedal structure. Our proof of strong global convergence refines many techniques currently in the literature and employs new ones that are of independent interest. With strong convergence established, we then present several stopping criteria and rigorously explore whether they will be triggered in finite time and supply bounds on false negative probabilities. Ultimately, we lay a foundation for rigorously developing stopping criteria for SGD methods for a broad class of functions, in hopes of making SGD a more complete optimization algorithm with greater adoption for data-driven problems.

The Impact of Local Geometry and Batch Size on Stochastic Gradient Descent for Nonconvex Problems

In several experimental reports on nonconvex optimization problems in machine learning, stochastic gradient descent (SGD) was observed to prefer minimizers with flat basins in comparison to more deterministic methods, yet there is very little rigorous understanding of this phenomenon. In fact, the lack of such work has led to an unverified, but widely-accepted stochastic mechanism describing why SGD prefers flatter minimizers to sharper minimizers. However, as we demonstrate, the stochastic mechanism fails to explain this phenomenon. Here, we propose an alternative deterministic mechanism that can accurately explain why SGD prefers flatter minimizers to sharper minimizers. We derive this mechanism based on a detailed analysis of a generic stochastic quadratic problem, which generalizes known results for classical gradient descent. Finally, we verify the predictions of our deterministic mechanism on two nonconvex problems.

On SGD's Failure in Practice: Characterizing and Overcoming Stalling

Stochastic Gradient Descent (SGD) is widely used in machine learning problems to efficiently perform empirical risk minimization, yet, in practice, SGD is known to stall before reaching the actual minimizer of the empirical risk. SGD stalling has often been attributed to its sensitivity to the conditioning of the problem; however, as we demonstrate, SGD will stall even when applied to a simple linear regression problem with unity condition number for standard learning rates. Thus, in this work, we numerically demonstrate and mathematically argue that stalling is a crippling and generic limitation of SGD and its variants in practice. Once we have established the problem of stalling, we generalize an existing framework for hedging against its effects, which (1) deters SGD and its variants from stalling, (2) still provides convergence guarantees, and (3) makes SGD and its variants more practical methods for minimization.

Kalman-based Stochastic Gradient Method with Stop Condition and Insensitivity to Conditioning

Modern proximal and stochastic gradient descent (SGD) methods are believed to efficiently minimize large composite objective functions, but such methods have two algorithmic challenges: (1) a lack of fast or justified stop conditions, and (2) sensitivity to the objective function's conditioning. In response to the first challenge, modern proximal and SGD methods guarantee convergence only after multiple epochs, but such a guarantee renders proximal and SGD methods infeasible when the number of component functions is very large or infinite. In response to the second challenge, second order SGD methods have been developed, but they are marred by the complexity of their analysis. In this work, we address these challenges on the limited, but important, linear regression problem by introducing and analyzing a second order proximal/SGD method based on Kalman Filtering (kSGD). Through our analysis, we show kSGD is asymptotically optimal, develop a fast algorithm for very large, infinite or streaming data sources with a justified stop condition, prove that kSGD is insensitive to the problem's conditioning, and develop a unique approach for analyzing the complex second order dynamics. Our theoretical results are supported by numerical experiments on three regression problems (linear, nonparametric wavelet, and logistic) using three large publicly available datasets. Moreover, our analysis and experiments lay a foundation for embedding kSGD in multiple epoch algorithms, extending kSGD to other problem classes, and developing parallel and low memory kSGD implementations.