Global Convergence and Stability of Stochastic Gradient Descent

In machine learning, stochastic gradient descent (SGD) is widely deployed to train models using highly non-convex objectives with equally complex noise models. Unfortunately, SGD theory often makes restrictive assumptions that fail to capture the non-convexity of real problems, and almost entirely ignore the complex noise models that exist in practice. In this work, we make substantial progress on this shortcoming. First, we establish that SGD's iterates will either globally converge to a stationary point or diverge under nearly arbitrary nonconvexity and noise models. Under a slightly more restrictive assumption on the joint behavior of the non-convexity and noise model that generalizes current assumptions in the literature, we show that the objective function cannot diverge, even if the iterates diverge. As a consequence of our results, SGD can be applied to a greater range of stochastic optimization problems with confidence about its global convergence behavior and stability.

Stochastic Approximation for High-frequency Observations in Data Assimilation

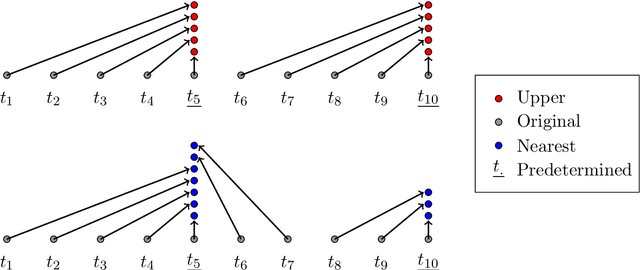
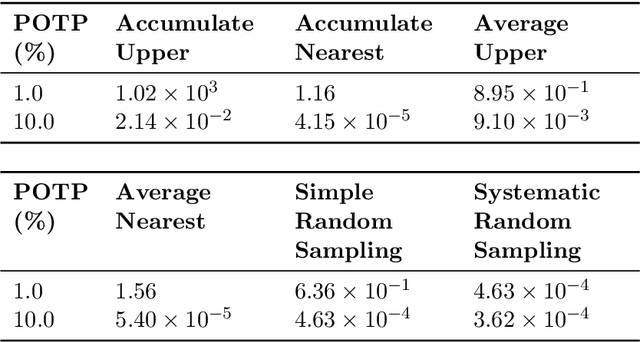
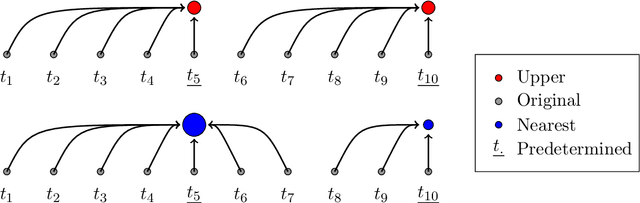
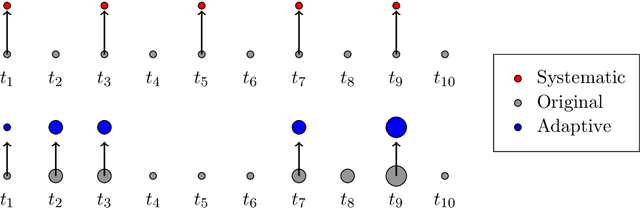
With the increasing penetration of high-frequency sensors across a number of biological and physical systems, the abundance of the resulting observations offers opportunities for higher statistical accuracy of down-stream estimates, but their frequency results in a plethora of computational problems in data assimilation tasks. The high-frequency of these observations has been traditionally dealt with by using data modification strategies such as accumulation, averaging, and sampling. However, these data modification strategies will reduce the quality of the estimates, which may be untenable for many systems. Therefore, to ensure high-quality estimates, we adapt stochastic approximation methods to address the unique challenges of high-frequency observations in data assimilation. As a result, we are able to produce estimates that leverage all of the observations in a manner that avoids the aforementioned computational problems and preserves the statistical accuracy of the estimates.