Stochastic Modified Flows, Mean-Field Limits and Dynamics of Stochastic Gradient Descent

We propose new limiting dynamics for stochastic gradient descent in the small learning rate regime called stochastic modified flows. These SDEs are driven by a cylindrical Brownian motion and improve the so-called stochastic modified equations by having regular diffusion coefficients and by matching the multi-point statistics. As a second contribution, we introduce distribution dependent stochastic modified flows which we prove to describe the fluctuating limiting dynamics of stochastic gradient descent in the small learning rate - infinite width scaling regime.

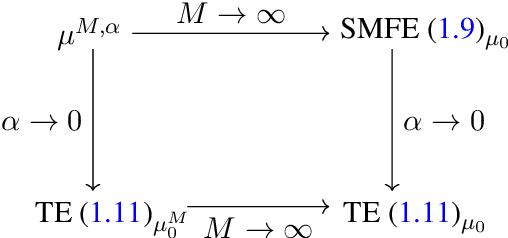
Conservative SPDEs as fluctuating mean field limits of stochastic gradient descent

The convergence of stochastic interacting particle systems in the mean-field limit to solutions to conservative stochastic partial differential equations is shown, with optimal rate of convergence. As a second main result, a quantitative central limit theorem for such SPDEs is derived, again with optimal rate of convergence. The results apply in particular to the convergence in the mean-field scaling of stochastic gradient descent dynamics in overparametrized, shallow neural networks to solutions to SPDEs. It is shown that the inclusion of fluctuations in the limiting SPDE improves the rate of convergence, and retains information about the fluctuations of stochastic gradient descent in the continuum limit.