Learning MR-Sort Models from Non-Monotone Data

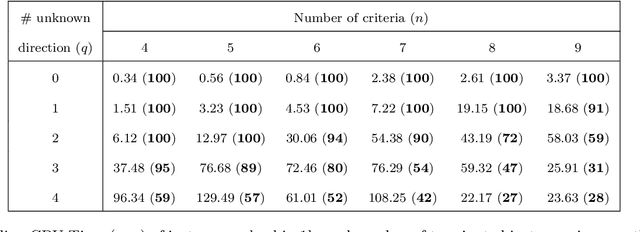
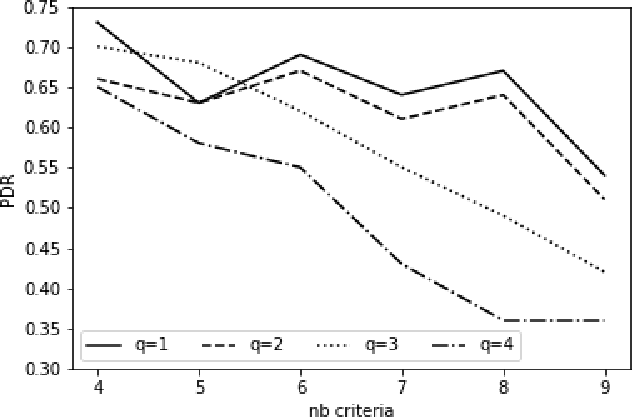
The Majority Rule Sorting (MR-Sort) method assigns alternatives evaluated on multiple criteria to one of the predefined ordered categories. The Inverse MR-Sort problem (Inv-MR-Sort) computes MR-Sort parameters that match a dataset. Existing learning algorithms for Inv-MR-Sort consider monotone preferences on criteria. We extend this problem to the case where the preferences on criteria are not necessarily monotone, but possibly single-peaked (or single-valley). We propose a mixed-integer programming based algorithm that learns the preferences on criteria together with the other MR-Sort parameters from the training data. We investigate the performance of the algorithm using numerical experiments and we illustrate its use on a real-world case study.

UTA-poly and UTA-splines: additive value functions with polynomial marginals

Additive utility function models are widely used in multiple criteria decision analysis. In such models, a numerical value is associated to each alternative involved in the decision problem. It is computed by aggregating the scores of the alternative on the different criteria of the decision problem. The score of an alternative is determined by a marginal value function that evolves monotonically as a function of the performance of the alternative on this criterion. Determining the shape of the marginals is not easy for a decision maker. It is easier for him/her to make statements such as "alternative $a$ is preferred to $b$". In order to help the decision maker, UTA disaggregation procedures use linear programming to approximate the marginals by piecewise linear functions based only on such statements. In this paper, we propose to infer polynomials and splines instead of piecewise linear functions for the marginals. In this aim, we use semidefinite programming instead of linear programming. We illustrate this new elicitation method and present some experimental results.