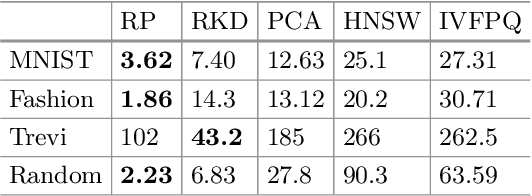
LoRANN: Low-Rank Matrix Factorization for Approximate Nearest Neighbor Search

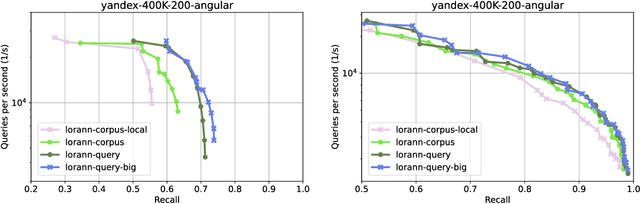
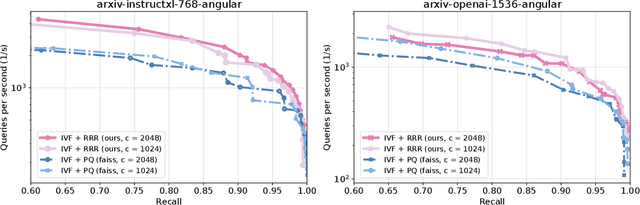
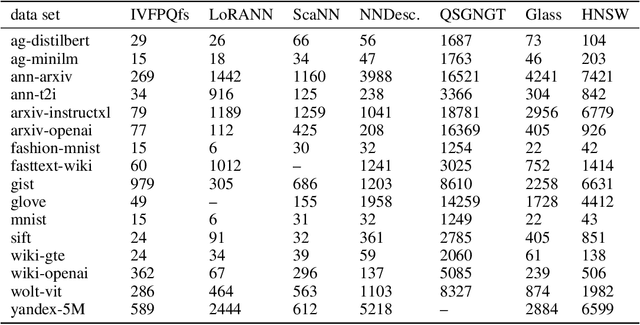
Approximate nearest neighbor (ANN) search is a key component in many modern machine learning pipelines; recent use cases include retrieval-augmented generation (RAG) and vector databases. Clustering-based ANN algorithms, that use score computation methods based on product quantization (PQ), are often used in industrial-scale applications due to their scalability and suitability for distributed and disk-based implementations. However, they have slower query times than the leading graph-based ANN algorithms. In this work, we propose a new supervised score computation method based on the observation that inner product approximation is a multivariate (multi-output) regression problem that can be solved efficiently by reduced-rank regression. Our experiments show that on modern high-dimensional data sets, the proposed reduced-rank regression (RRR) method is superior to PQ in both query latency and memory usage. We also introduce LoRANN, a clustering-based ANN library that leverages the proposed score computation method. LoRANN is competitive with the leading graph-based algorithms and outperforms the state-of-the-art GPU ANN methods on high-dimensional data sets.

Supervised Learning Approach to Approximate Nearest Neighbor Search

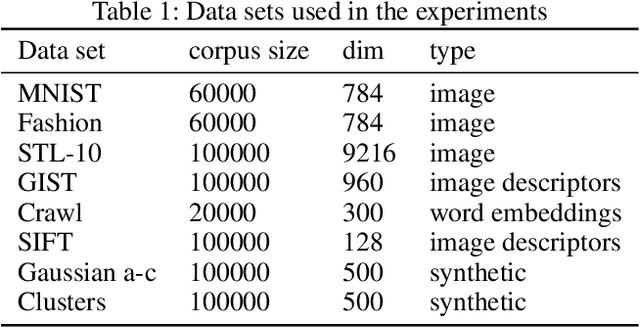
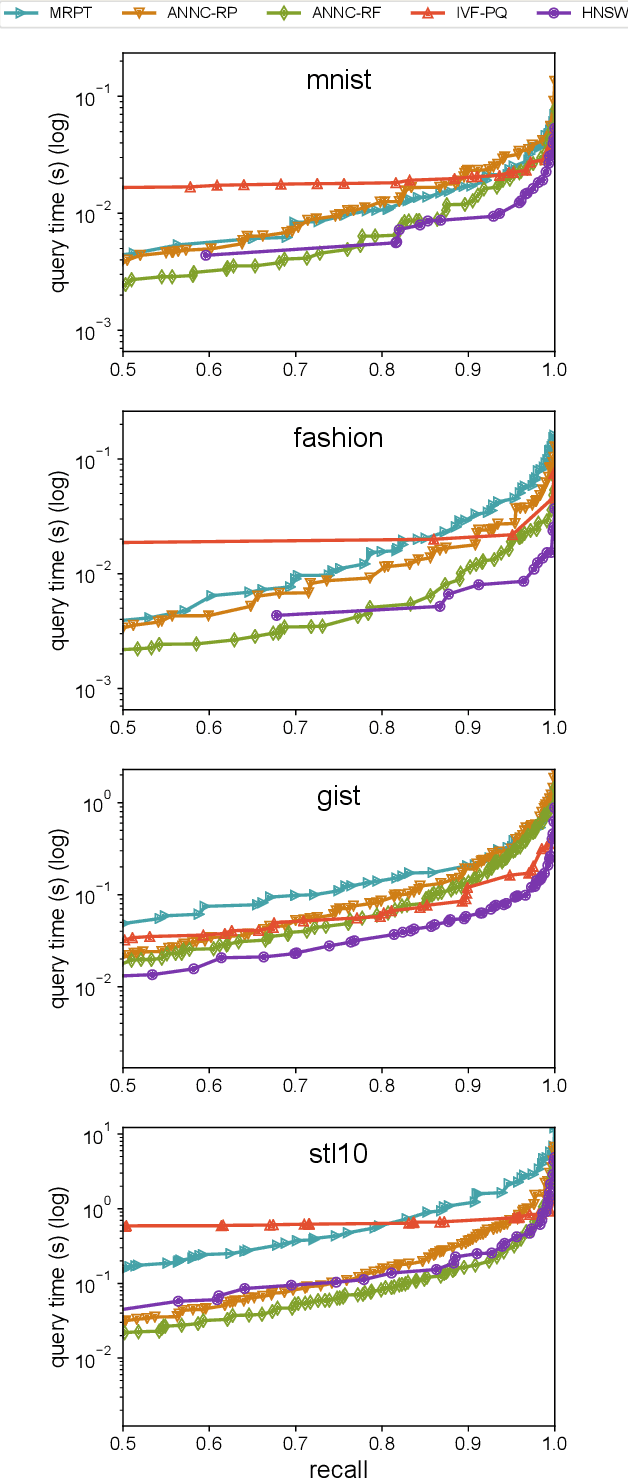
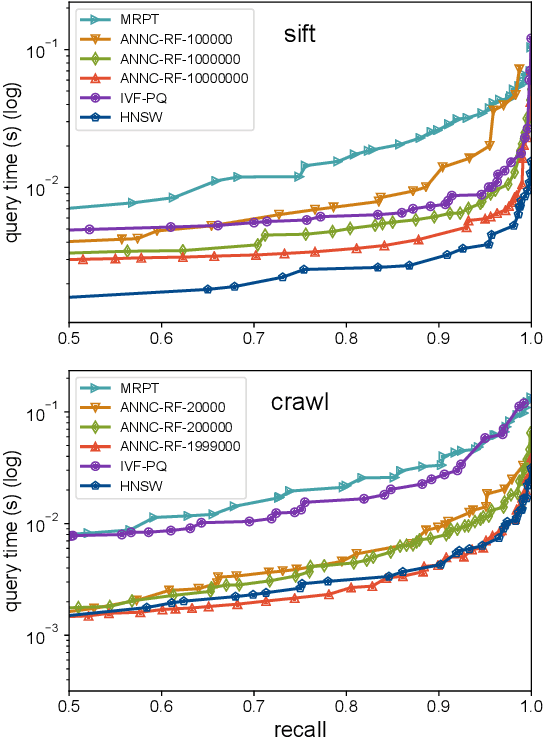
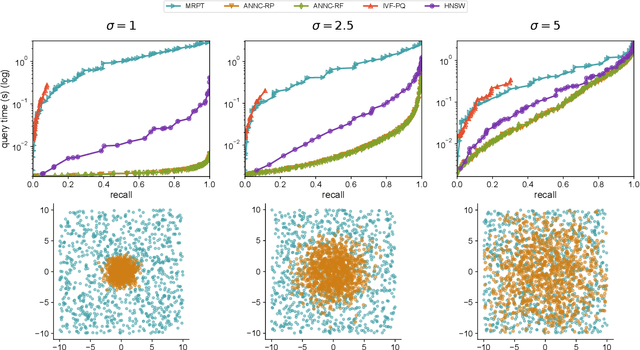
Approximate nearest neighbor search is a classic algorithmic problem where the goal is to design an efficient index structure for fast approximate nearest neighbor queries. We show that it can be framed as a classification problem and solved by training a suitable multi-label classifier and using it as an index. Compared to the existing algorithms, this supervised learning approach has several advantages: it enables adapting an index to the query distribution when the query distribution and the corpus distribution differ; it allows using training sets larger than the corpus; and in principle it enables using any multi-label classifier for approximate nearest neighbor search. We demonstrate these advantages on multiple synthetic and real-world data sets by using a random forest and an ensemble of random projection trees as the base classifiers.

Efficient Autotuning of Hyperparameters in Approximate Nearest Neighbor Search

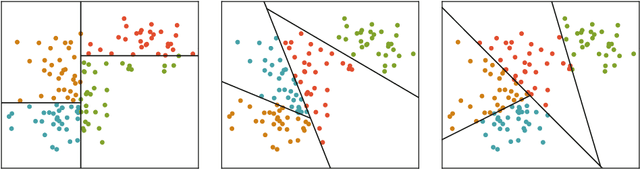
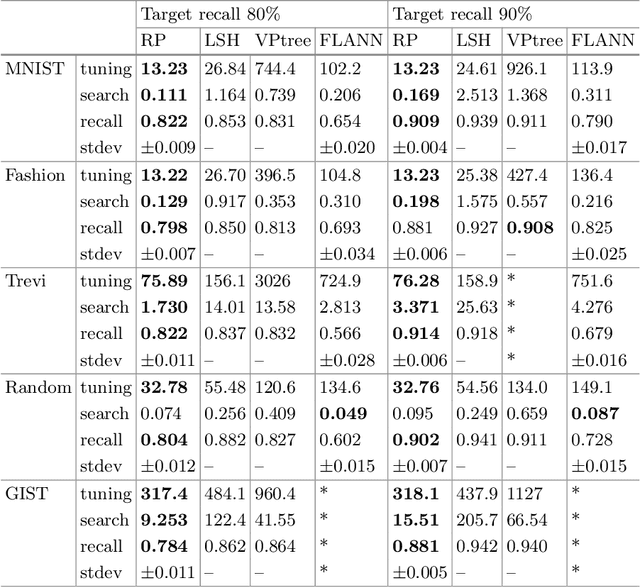
Approximate nearest neighbor algorithms are used to speed up nearest neighbor search in a wide array of applications. However, current indexing methods feature several hyperparameters that need to be tuned to reach an acceptable accuracy--speed trade-off. A grid search in the parameter space is often impractically slow due to a time-consuming index-building procedure. Therefore, we propose an algorithm for automatically tuning the hyperparameters of indexing methods based on randomized space-partitioning trees. In particular, we present results using randomized k-d trees, random projection trees and randomized PCA trees. The tuning algorithm adds minimal overhead to the index-building process but is able to find the optimal hyperparameters accurately. We demonstrate that the algorithm is significantly faster than existing approaches, and that the indexing methods used are competitive with the state-of-the-art methods in query time while being faster to build.

Fast k-NN search

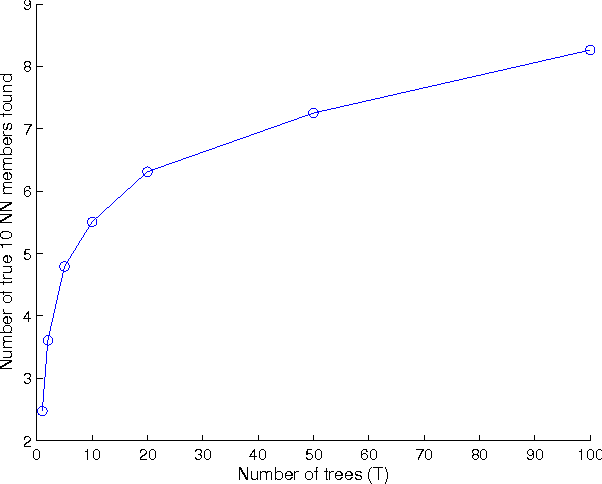
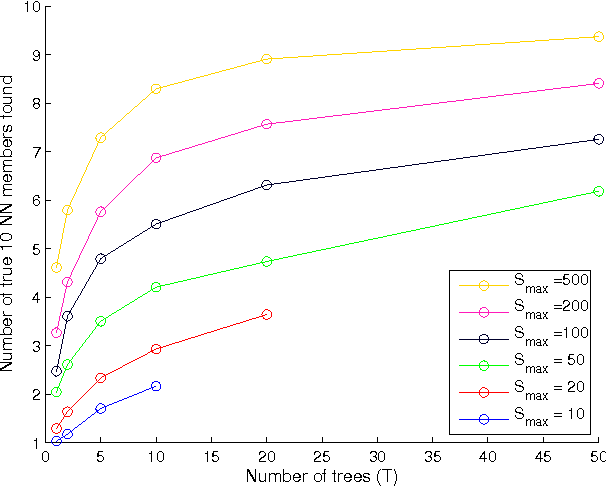
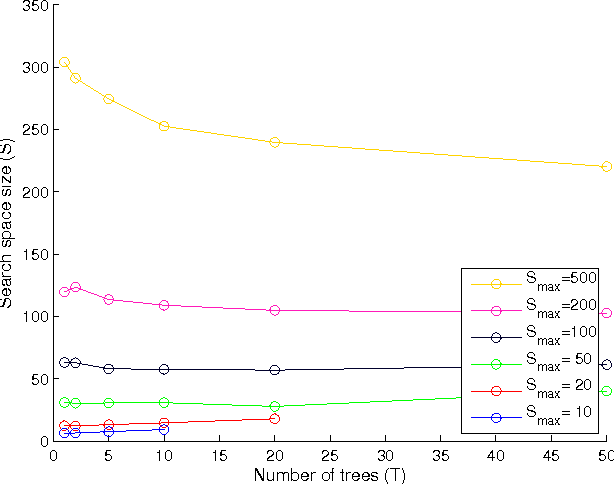
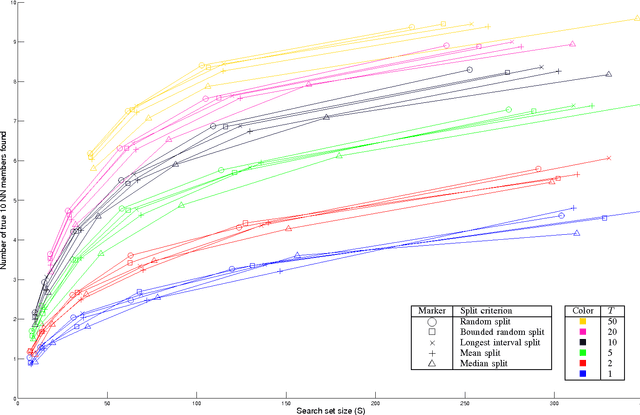
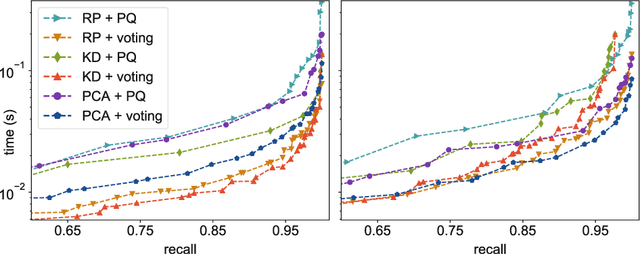
Efficient index structures for fast approximate nearest neighbor queries are required in many applications such as recommendation systems. In high-dimensional spaces, many conventional methods suffer from excessive usage of memory and slow response times. We propose a method where multiple random projection trees are combined by a novel voting scheme. The key idea is to exploit the redundancy in a large number of candidate sets obtained by independently generated random projections in order to reduce the number of expensive exact distance evaluations. The method is straightforward to implement using sparse projections which leads to a reduced memory footprint and fast index construction. Furthermore, it enables grouping of the required computations into big matrix multiplications, which leads to additional savings due to cache effects and low-level parallelization. We demonstrate by extensive experiments on a wide variety of data sets that the method is faster than existing partitioning tree or hashing based approaches, making it the fastest available technique on high accuracy levels.