Can sparse autoencoders make sense of latent representations?

Sparse autoencoders (SAEs) have lately been used to uncover interpretable latent features in large language models. Here, we explore their potential for decomposing latent representations in complex and high-dimensional biological data, where the underlying variables are often unknown. On simulated data we show that generative hidden variables can be captured in learned representations in the form of superpositions. The degree to which they are learned depends on the completeness of the representations. Superpositions, however, are not identifiable if these generative variables are unknown. SAEs can to some extent recover these variables, yielding interpretable features. Applied to single-cell multi-omics data, we show that an SAE can uncover key biological processes such as carbon dioxide transport and ion homeostasis, which are crucial for red blood cell differentiation and immune function. Our findings highlight how SAEs can be used in advancing interpretability in biological and other scientific domains.

The deep generative decoder: Using MAP estimates of representations

A deep generative model is characterized by a representation space, its distribution, and a neural network mapping the representation to a distribution over vectors in feature space. Common methods such as variational autoencoders (VAEs) apply variational inference for training the neural network, but optimizing these models is often non-trivial. The encoder adds to the complexity of the model and introduces an amortization gap and the quality of the variational approximation is usually unknown. Additionally, the balance of the loss terms of the objective function heavily influences performance. Therefore, we argue that it is worthwhile to investigate a much simpler approximation which finds representations and their distribution by maximizing the model likelihood via back-propagation. In this approach, there is no encoder, and we therefore call it a Deep Generative Decoder (DGD). Using the CIFAR10 data set, we show that the DGD is easier and faster to optimize than the VAE, achieves more consistent low reconstruction errors of test data, and alleviates the problem of balancing the reconstruction and distribution loss terms. Although the model in its simple form cannot compete with state-of-the-art image generation approaches, it obtains better image generation scores than the variational approach on the CIFAR10 data. We demonstrate on MNIST data how the use of a Gaussian mixture with priors can lead to a clear separation of classes in a 2D representation space, and how the DGD can be used with labels to obtain a supervised representation.

A manifold learning perspective on representation learning: Learning decoder and representations without an encoder

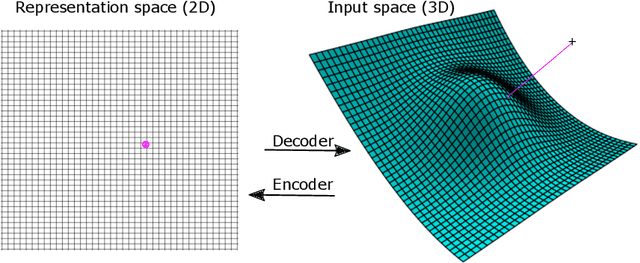
Autoencoders are commonly used in representation learning. They consist of an encoder and a decoder, which provide a straightforward way to map $n$-dimensional data in input space to a lower $m$-dimensional representation space and back. The decoder itself defines an $m$-dimensional manifold in input space. Inspired by manifold learning, we show that the decoder can be trained on its own by learning the representations of the training samples along with the decoder weights using gradient descent. A sum-of-squares loss then corresponds to optimizing the manifold to have the smallest Euclidean distance to the training samples, and similarly for other loss functions. We derive expressions for the number of samples needed to specify the encoder and decoder and show that the decoder generally requires much less training samples to be well-specified compared to the encoder. We discuss training of autoencoders in this perspective and relate to previous work in the field that use noisy training examples and other types of regularization. On the natural image data sets MNIST and CIFAR10, we demonstrate that the decoder is much better suited to learn a low-dimensional representation, especially when trained on small data sets. Using simulated gene regulatory data, we further show that the decoder alone leads to better generalization and meaningful representations. Our approach of training the decoder alone facilitates representation learning even on small data sets and can lead to improved training of autoencoders. We hope that the simple analyses presented will also contribute to an improved conceptual understanding of representation learning.