A manifold learning perspective on representation learning: Learning decoder and representations without an encoder

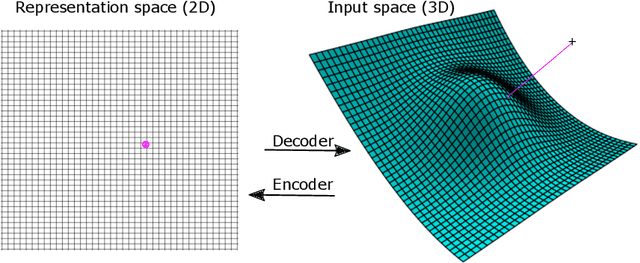
Autoencoders are commonly used in representation learning. They consist of an encoder and a decoder, which provide a straightforward way to map $n$-dimensional data in input space to a lower $m$-dimensional representation space and back. The decoder itself defines an $m$-dimensional manifold in input space. Inspired by manifold learning, we show that the decoder can be trained on its own by learning the representations of the training samples along with the decoder weights using gradient descent. A sum-of-squares loss then corresponds to optimizing the manifold to have the smallest Euclidean distance to the training samples, and similarly for other loss functions. We derive expressions for the number of samples needed to specify the encoder and decoder and show that the decoder generally requires much less training samples to be well-specified compared to the encoder. We discuss training of autoencoders in this perspective and relate to previous work in the field that use noisy training examples and other types of regularization. On the natural image data sets MNIST and CIFAR10, we demonstrate that the decoder is much better suited to learn a low-dimensional representation, especially when trained on small data sets. Using simulated gene regulatory data, we further show that the decoder alone leads to better generalization and meaningful representations. Our approach of training the decoder alone facilitates representation learning even on small data sets and can lead to improved training of autoencoders. We hope that the simple analyses presented will also contribute to an improved conceptual understanding of representation learning.