Using Latent Binary Variables for Online Reconstruction of Large Scale Systems

We propose a probabilistic graphical model realizing a minimal encoding of real variables dependencies based on possibly incomplete observation and an empirical cumulative distribution function per variable. The target application is a large scale partially observed system, like e.g. a traffic network, where a small proportion of real valued variables are observed, and the other variables have to be predicted. Our design objective is therefore to have good scalability in a real-time setting. Instead of attempting to encode the dependencies of the system directly in the description space, we propose a way to encode them in a latent space of binary variables, reflecting a rough perception of the observable (congested/non-congested for a traffic road). The method relies in part on message passing algorithms, i.e. belief propagation, but the core of the work concerns the definition of meaningful latent variables associated to the variables of interest and their pairwise dependencies. Numerical experiments demonstrate the applicability of the method in practice.

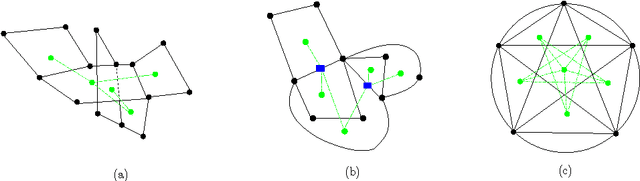
Pairwise MRF Calibration by Perturbation of the Bethe Reference Point

We investigate different ways of generating approximate solutions to the pairwise Markov random field (MRF) selection problem. We focus mainly on the inverse Ising problem, but discuss also the somewhat related inverse Gaussian problem because both types of MRF are suitable for inference tasks with the belief propagation algorithm (BP) under certain conditions. Our approach consists in to take a Bethe mean-field solution obtained with a maximum spanning tree (MST) of pairwise mutual information, referred to as the \emph{Bethe reference point}, for further perturbation procedures. We consider three different ways following this idea: in the first one, we select and calibrate iteratively the optimal links to be added starting from the Bethe reference point; the second one is based on the observation that the natural gradient can be computed analytically at the Bethe point; in the third one, assuming no local field and using low temperature expansion we develop a dual loop joint model based on a well chosen fundamental cycle basis. We indeed identify a subclass of planar models, which we refer to as \emph{Bethe-dual graph models}, having possibly many loops, but characterized by a singly connected dual factor graph, for which the partition function and the linear response can be computed exactly in respectively O(N) and $O(N^2)$ operations, thanks to a dual weight propagation (DWP) message passing procedure that we set up. When restricted to this subclass of models, the inverse Ising problem being convex, becomes tractable at any temperature. Experimental tests on various datasets with refined $L_0$ or $L_1$ regularization procedures indicate that these approaches may be competitive and useful alternatives to existing ones.

Local stability of Belief Propagation algorithm with multiple fixed points

A number of problems in statistical physics and computer science can be expressed as the computation of marginal probabilities over a Markov random field. Belief propagation, an iterative message-passing algorithm, computes exactly such marginals when the underlying graph is a tree. But it has gained its popularity as an efficient way to approximate them in the more general case, even if it can exhibits multiple fixed points and is not guaranteed to converge. In this paper, we express a new sufficient condition for local stability of a belief propagation fixed point in terms of the graph structure and the beliefs values at the fixed point. This gives credence to the usual understanding that Belief Propagation performs better on sparse graphs.

The Role of Normalization in the Belief Propagation Algorithm

An important part of problems in statistical physics and computer science can be expressed as the computation of marginal probabilities over a Markov Random Field. The belief propagation algorithm, which is an exact procedure to compute these marginals when the underlying graph is a tree, has gained its popularity as an efficient way to approximate them in the more general case. In this paper, we focus on an aspect of the algorithm that did not get that much attention in the literature, which is the effect of the normalization of the messages. We show in particular that, for a large class of normalization strategies, it is possible to focus only on belief convergence. Following this, we express the necessary and sufficient conditions for local stability of a fixed point in terms of the graph structure and the beliefs values at the fixed point. We also explicit some connexion between the normalization constants and the underlying Bethe Free Energy.