MaCE: General Mass Conserving Dynamics for Cellular Automata

We present Mass-Conserving Evolution (MaCE), a general method for implementing mass conservation in Cellular Automata (CA). MaCE is a simple evolution rule that can be easily 'attached' to existing CAs to make them mass-conserving, which tends to produce interesting behaviours more often, as patterns can no longer explode or die out. We first show that MaCE is numerically stable and admits a simple continuous limit. We then test MaCE on Lenia, and through several experiments, we demonstrate that it produces a wide variety of interesting behaviours, starting from the variety and abundance of solitons up to hints of intrinsic evolution in resource-constrained environments. Finally, we showcase the versatility of MaCE by applying it to Neural-CAs and discrete CAs, and discuss promising research directions opened up by this scheme.

Looking for Complexity at Phase Boundaries in Continuous Cellular Automata

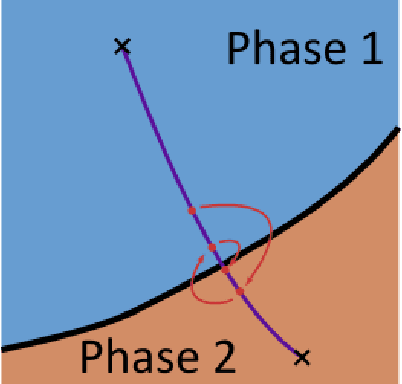
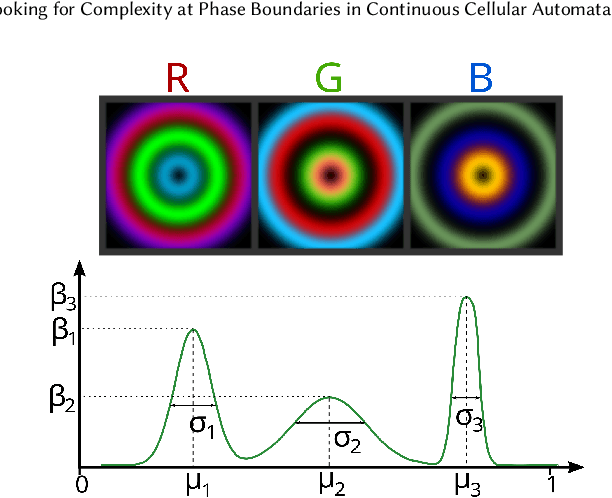
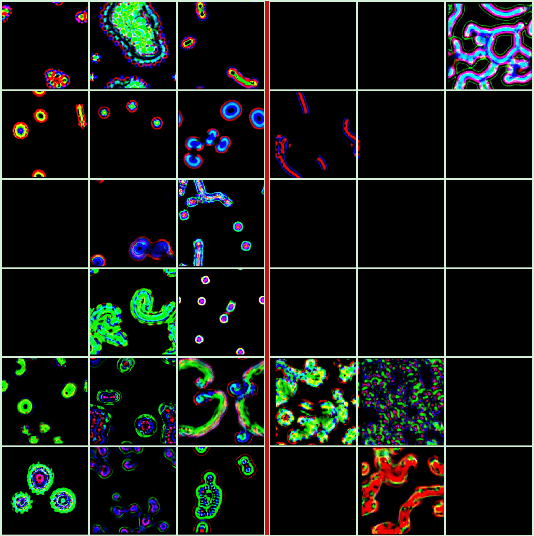
One key challenge in Artificial Life is designing systems that display an emergence of complex behaviors. Many such systems depend on a high-dimensional parameter space, only a small subset of which displays interesting dynamics. Focusing on the case of continuous systems, we introduce the 'Phase Transition Finder'(PTF) algorithm, which can be used to efficiently generate parameters lying at the border between two phases. We argue that such points are more likely to display complex behaviors, and confirm this by applying PTF to Lenia showing it can increase the frequency of interesting behaviors more than two-fold, while remaining efficient enough for large-scale searches.

Arrows of Time for Large Language Models

We study the probabilistic modeling performed by Autoregressive Large Language Models through the angle of time directionality. We empirically find a time asymmetry exhibited by such models in their ability to model natural language: a difference in the average log-perplexity when trying to predict the next token versus when trying to predict the previous one. This difference is at the same time subtle and very consistent across various modalities (language, model size, training time, ...). Theoretically, this is surprising: from an information-theoretic point of view, there should be no such difference. We provide a theoretical framework to explain how such an asymmetry can appear from sparsity and computational complexity considerations, and outline a number of perspectives opened by our results.