Looking for Complexity at Phase Boundaries in Continuous Cellular Automata
Paper and Code
Mar 08, 2024
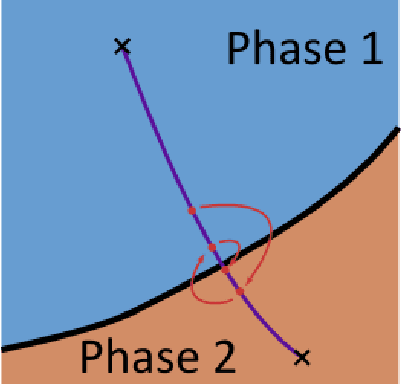
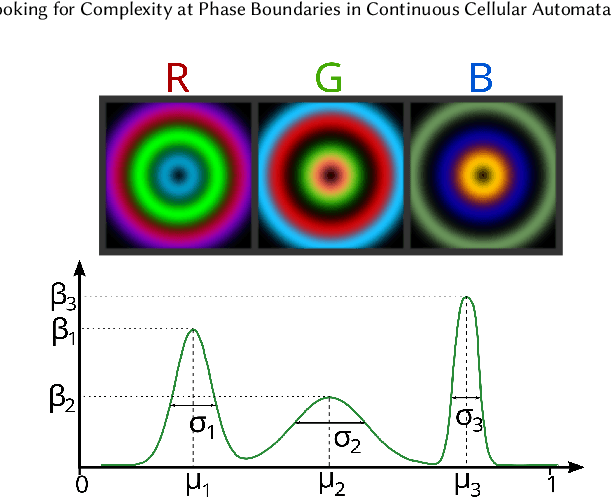
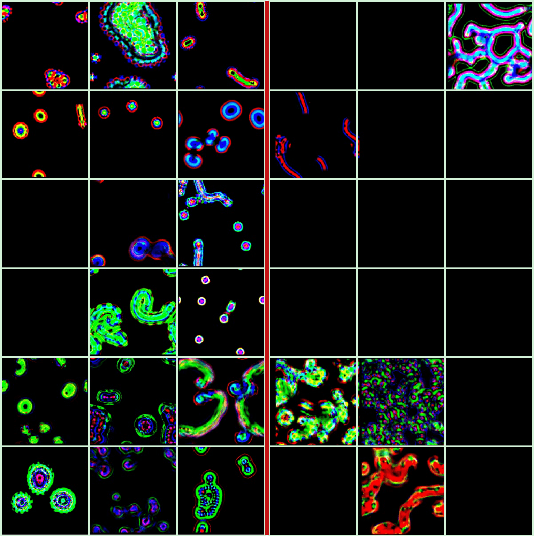
One key challenge in Artificial Life is designing systems that display an emergence of complex behaviors. Many such systems depend on a high-dimensional parameter space, only a small subset of which displays interesting dynamics. Focusing on the case of continuous systems, we introduce the 'Phase Transition Finder'(PTF) algorithm, which can be used to efficiently generate parameters lying at the border between two phases. We argue that such points are more likely to display complex behaviors, and confirm this by applying PTF to Lenia showing it can increase the frequency of interesting behaviors more than two-fold, while remaining efficient enough for large-scale searches.
* 5 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge