Spot the bot: Coarse-Grained Partition of Semantic Paths for Bots and Humans

Nowadays, technology is rapidly advancing: bots are writing comments, articles, and reviews. Due to this fact, it is crucial to know if the text was written by a human or by a bot. This paper focuses on comparing structures of the coarse-grained partitions of semantic paths for human-written and bot-generated texts. We compare the clusterizations of datasets of n-grams from literary texts and texts generated by several bots. The hypothesis is that the structures and clusterizations are different. Our research supports the hypothesis. As the semantic structure may be different for different languages, we investigate Russian, English, German, and Vietnamese languages.

A Language and Its Dimensions: Intrinsic Dimensions of Language Fractal Structures

The present paper introduces a novel object of study - a language fractal structure. We hypothesize that a set of embeddings of all $n$-grams of a natural language constitutes a representative sample of this fractal set. (We use the term Hailonakea to refer to the sum total of all language fractal structures, over all $n$). The paper estimates intrinsic (genuine) dimensions of language fractal structures for the Russian and English languages. To this end, we employ methods based on (1) topological data analysis and (2) a minimum spanning tree of a data graph for a cloud of points considered (Steele theorem). For both languages, for all $n$, the intrinsic dimensions appear to be non-integer values (typical for fractal sets), close to 9 for both of the Russian and English language.

Formal concept analysis for evaluating intrinsic dimension of a natural language

Some results of a computational experiment for determining the intrinsic dimension of linguistic varieties for the Bengali and Russian languages are presented. At the same time, both sets of words and sets of bigrams in these languages were considered separately. The method used to solve this problem was based on formal concept analysis algorithms. It was found that the intrinsic dimensions of these languages are significantly less than the dimensions used in popular neural network models in natural language processing.

Genetic Engineering Algorithm (GEA): An Efficient Metaheuristic Algorithm for Solving Combinatorial Optimization Problems

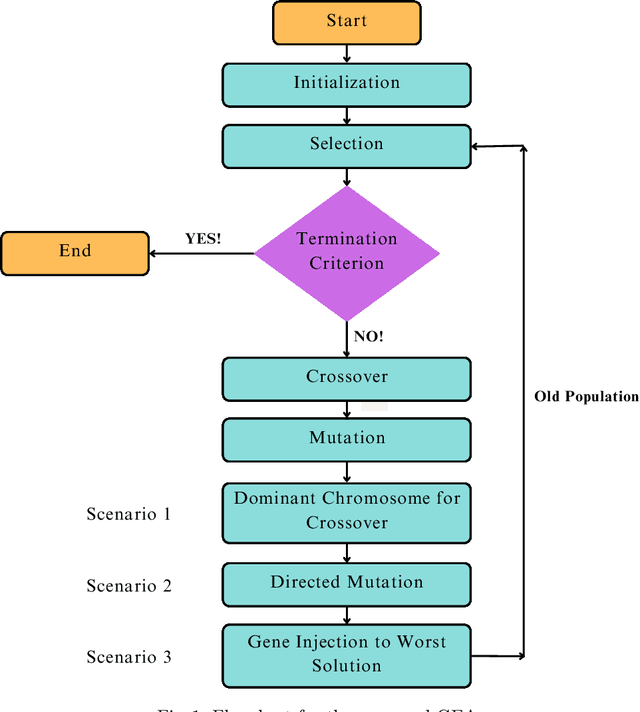
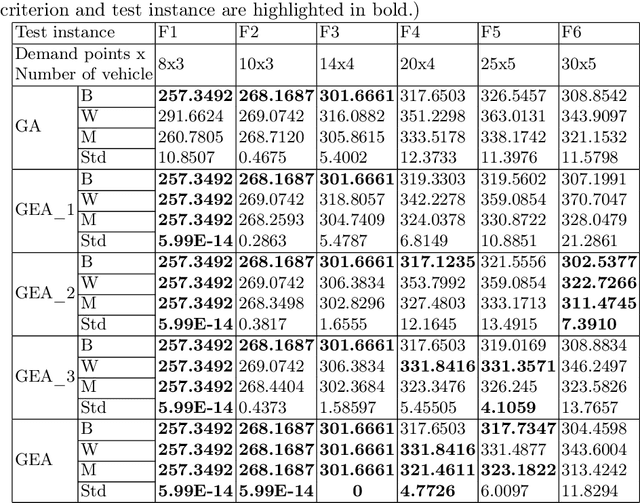
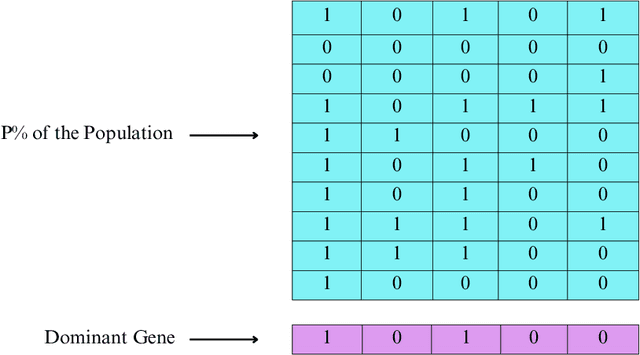
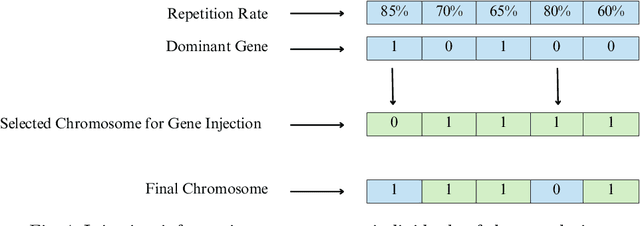
Genetic Algorithms (GAs) are known for their efficiency in solving combinatorial optimization problems, thanks to their ability to explore diverse solution spaces, handle various representations, exploit parallelism, preserve good solutions, adapt to changing dynamics, handle combinatorial diversity, and provide heuristic search. However, limitations such as premature convergence, lack of problem-specific knowledge, and randomness of crossover and mutation operators make GAs generally inefficient in finding an optimal solution. To address these limitations, this paper proposes a new metaheuristic algorithm called the Genetic Engineering Algorithm (GEA) that draws inspiration from genetic engineering concepts. GEA redesigns the traditional GA while incorporating new search methods to isolate, purify, insert, and express new genes based on existing ones, leading to the emergence of desired traits and the production of specific chromosomes based on the selected genes. Comparative evaluations against state-of-the-art algorithms on benchmark instances demonstrate the superior performance of GEA, showcasing its potential as an innovative and efficient solution for combinatorial optimization problems.

Date-Driven Approach for Identifying State of Hemodialysis Fistulas: Entropy-Complexity and Formal Concept Analysis

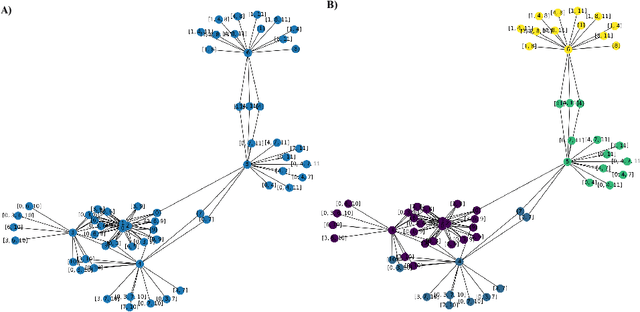
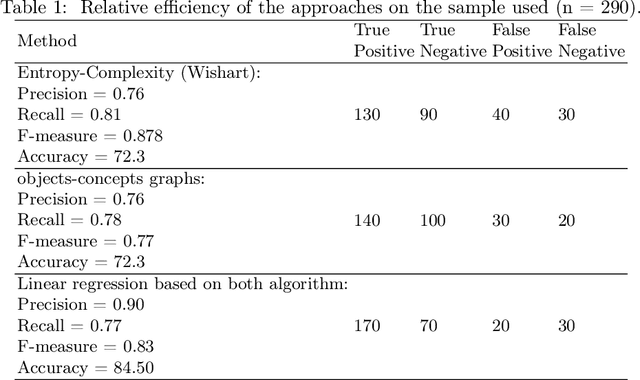
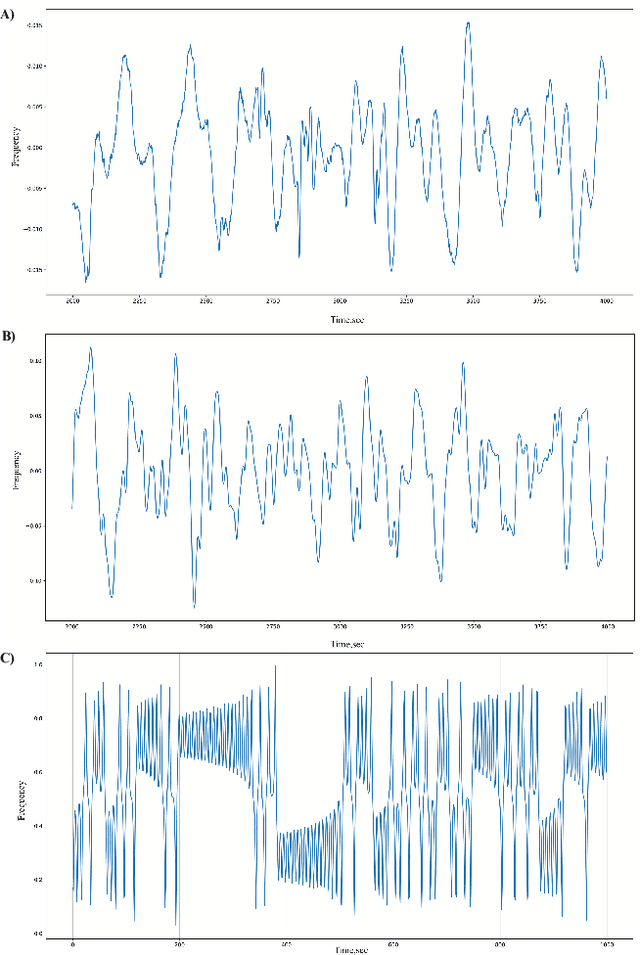
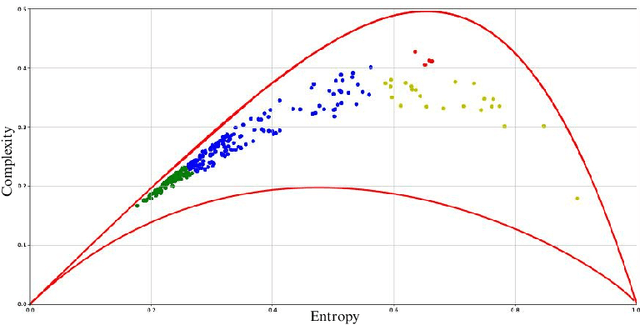
The paper explores mathematical methods that differentiate regular and chaotic time series, specifically for identifying pathological fistulas. It proposes a noise-resistant method for classifying responding rows of normally and pathologically functioning fistulas. This approach is grounded in the hypothesis that laminar blood flow signifies normal function, while turbulent flow indicates pathology. The study explores two distinct methods for distinguishing chaotic from regular time series. The first method involves mapping the time series onto the entropy-complexity plane and subsequently comparing it to established clusters. The second method, introduced by the authors, constructs a concepts-objects graph using formal concept analysis. Both of these methods exhibit high efficiency in determining the state of the fistula.