Gauge-invariant representation holonomy

Deep networks learn internal representations whose geometry--how features bend, rotate, and evolve--affects both generalization and robustness. Existing similarity measures such as CKA or SVCCA capture pointwise overlap between activation sets, but miss how representations change along input paths. Two models may appear nearly identical under these metrics yet respond very differently to perturbations or adversarial stress. We introduce representation holonomy, a gauge-invariant statistic that measures this path dependence. Conceptually, holonomy quantifies the "twist" accumulated when features are parallel-transported around a small loop in input space: flat representations yield zero holonomy, while nonzero values reveal hidden curvature. Our estimator fixes gauge through global whitening, aligns neighborhoods using shared subspaces and rotation-only Procrustes, and embeds the result back to the full feature space. We prove invariance to orthogonal (and affine, post-whitening) transformations, establish a linear null for affine layers, and show that holonomy vanishes at small radii. Empirically, holonomy increases with loop radius, separates models that appear similar under CKA, and correlates with adversarial and corruption robustness. It also tracks training dynamics as features form and stabilize. Together, these results position representation holonomy as a practical and scalable diagnostic for probing the geometric structure of learned representations beyond pointwise similarity.

Training Memory in Deep Neural Networks: Mechanisms, Evidence, and Measurement Gaps

Modern deep-learning training is not memoryless. Updates depend on optimizer moments and averaging, data-order policies (random reshuffling vs with-replacement, staged augmentations and replay), the nonconvex path, and auxiliary state (teacher EMA/SWA, contrastive queues, BatchNorm statistics). This survey organizes mechanisms by source, lifetime, and visibility. It introduces seed-paired, function-space causal estimands; portable perturbation primitives (carry/reset of momentum/Adam/EMA/BN, order-window swaps, queue/teacher tweaks); and a reporting checklist with audit artifacts (order hashes, buffer/BN checksums, RNG contracts). The conclusion is a protocol for portable, causal, uncertainty-aware measurement that attributes how much training history matters across models, data, and regimes.

Process-Tensor Tomography of SGD: Measuring Non-Markovian Memory via Back-Flow of Distinguishability

This work proposes neural training as a \emph{process tensor}: a multi-time map that takes a sequence of controllable instruments (batch choices, augmentations, optimizer micro-steps) and returns an observable of the trained model. Building on this operational lens, we introduce a simple, model-agnostic witness of training memory based on \emph{back-flow of distinguishability}. In a controlled two-step protocol, we compare outcome distributions after one intervention versus two; the increase $Δ_{\mathrm{BF}} = D_2 - D_1>0$ (with $D\in\{\mathrm{TV}, \mathrm{JS}, \mathrm{H}\}$ measured on softmax predictions over a fixed probe set) certifies non-Markovianity. We observe consistent positive back-flow with tight bootstrap confidence intervals, amplification under higher momentum, larger batch overlap, and more micro-steps, and collapse under a \emph{causal break} (resetting optimizer state), directly attributing the effect to optimizer/data-state memory. The witness is robust across TV/JS/Hellinger, inexpensive to compute, and requires no architectural changes. We position this as a \emph{measurement} contribution: a principled diagnostic and empirical evidence that practical SGD deviates from the Markov idealization. An exploratory case study illustrates how the micro-level signal can inform curriculum orderings. "Data order matters" turns into a testable operator with confidence bounds, our framework offers a common stage to compare optimizers, curricula, and schedules through their induced training memory.

Deep learning based black spot identification on Greek road networks

Black spot identification, a spatiotemporal phenomenon, involves analyzing the geographical location and time-based occurrence of road accidents. Typically, this analysis examines specific locations on road networks during set time periods to pinpoint areas with a higher concentration of accidents, known as black spots. By evaluating these problem areas, researchers can uncover the underlying causes and reasons for increased collision rates, such as road design, traffic volume, driver behavior, weather, and infrastructure. However, challenges in identifying black spots include limited data availability, data quality, and assessing contributing factors. Additionally, evolving road design, infrastructure, and vehicle safety technology can affect black spot analysis and determination. This study focused on traffic accidents in Greek road networks to recognize black spots, utilizing data from police and government-issued car crash reports. The study produced a publicly available dataset called Black Spots of North Greece (BSNG) and a highly accurate identification method.

Defect detection using weakly supervised learning

In many real-world scenarios, obtaining large amounts of labeled data can be a daunting task. Weakly supervised learning techniques have gained significant attention in recent years as an alternative to traditional supervised learning, as they enable training models using only a limited amount of labeled data. In this paper, the performance of a weakly supervised classifier to its fully supervised counterpart is compared on the task of defect detection. Experiments are conducted on a dataset of images containing defects, and evaluate the two classifiers based on their accuracy, precision, and recall. Our results show that the weakly supervised classifier achieves comparable performance to the supervised classifier, while requiring significantly less labeled data.

Dens-PU: PU Learning with Density-Based Positive Labeled Augmentation

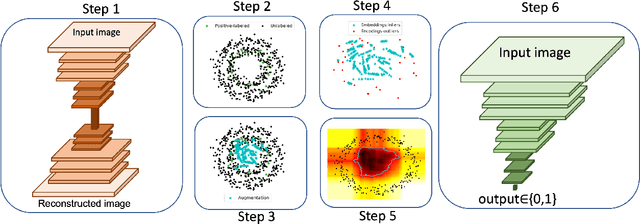
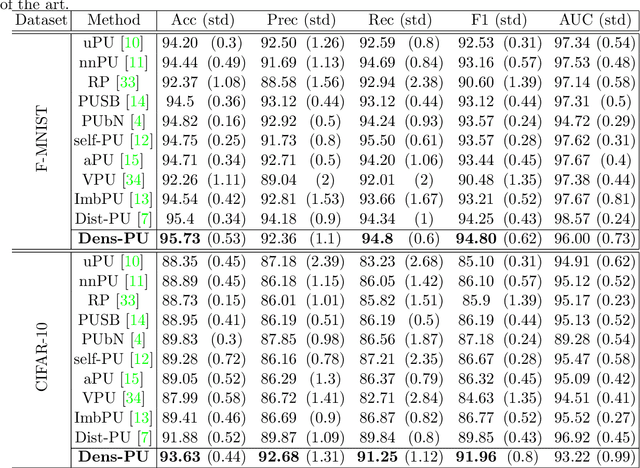
This study proposes a novel approach for solving the PU learning problem based on an anomaly-detection strategy. Latent encodings extracted from positive-labeled data are linearly combined to acquire new samples. These new samples are used as embeddings to increase the density of positive-labeled data and, thus, define a boundary that approximates the positive class. The further a sample is from the boundary the more it is considered as a negative sample. Once a set of negative samples is obtained, the PU learning problem reduces to binary classification. The approach, named Dens-PU due to its reliance on the density of positive-labeled data, was evaluated using benchmark image datasets, and state-of-the-art results were attained.