PearSAN: A Machine Learning Method for Inverse Design using Pearson Correlated Surrogate Annealing

PearSAN is a machine learning-assisted optimization algorithm applicable to inverse design problems with large design spaces, where traditional optimizers struggle. The algorithm leverages the latent space of a generative model for rapid sampling and employs a Pearson correlated surrogate model to predict the figure of merit of the true design metric. As a showcase example, PearSAN is applied to thermophotovoltaic (TPV) metasurface design by matching the working bands between a thermal radiator and a photovoltaic cell. PearSAN can work with any pretrained generative model with a discretized latent space, making it easy to integrate with VQ-VAEs and binary autoencoders. Its novel Pearson correlational loss can be used as both a latent regularization method, similar to batch and layer normalization, and as a surrogate training loss. We compare both to previous energy matching losses, which are shown to enforce poor regularization and performance, even with upgraded affine parameters. PearSAN achieves a state-of-the-art maximum design efficiency of 97%, and is at least an order of magnitude faster than previous methods, with an improved maximum figure-of-merit gain.

A Relative Church-Turing-Deutsch Thesis from Special Relativity and Undecidability

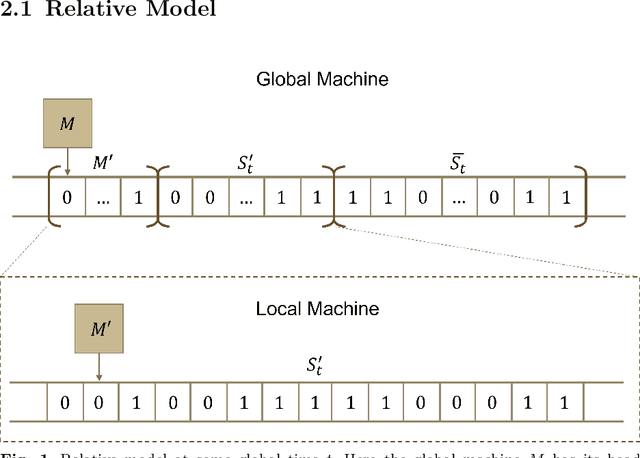
Beginning with Turing's seminal work in 1950, artificial intelligence proposes that consciousness can be simulated by a Turing machine. This implies a potential theory of everything where the universe is a simulation on a computer, which begs the question of whether we can prove we exist in a simulation. In this work, we construct a relative model of computation where a computable \textit{local} machine is simulated by a \textit{global}, classical Turing machine. We show that the problem of the local machine computing \textbf{simulation properties} of its global simulator is undecidable in the same sense as the Halting problem. Then, we show that computing the time, space, or error accumulated by the global simulator are simulation properties and therefore are undecidable. These simulation properties give rise to special relativistic effects in the relative model which we use to construct a relative Church-Turing-Deutsch thesis where a global, classical Turing machine computes quantum mechanics for a local machine with the same constant-time local computational complexity as experienced in our universe.