V. R. Lalchand
Physics-informed Gaussian Process for Online Optimization of Particle Accelerators
Sep 08, 2020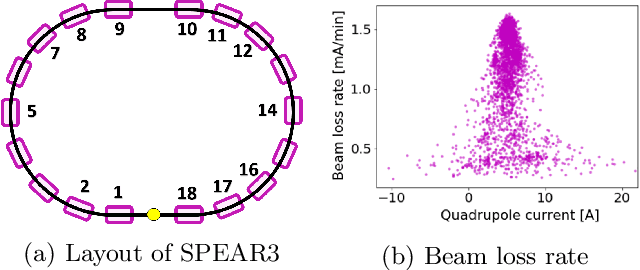
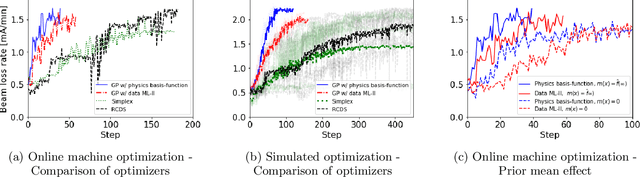
Abstract:High-dimensional optimization is a critical challenge for operating large-scale scientific facilities. We apply a physics-informed Gaussian process (GP) optimizer to tune a complex system by conducting efficient global search. Typical GP models learn from past observations to make predictions, but this reduces their applicability to new systems where archive data is not available. Instead, here we use a fast approximate model from physics simulations to design the GP model. The GP is then employed to make inferences from sequential online observations in order to optimize the system. Simulation and experimental studies were carried out to demonstrate the method for online control of a storage ring. We show that the physics-informed GP outperforms current routinely used online optimizers in terms of convergence speed, and robustness on this task. The ability to inform the machine-learning model with physics may have wide applications in science.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge